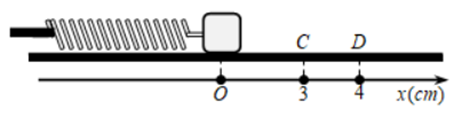
Cho cơ hệ như hình vẽ: lò xo có độ cứng k = 100 N/m, vật nặng khối lượng m = 100 g bề mặt chỉ có ma sát trên đoạn CD, biết CD = 1 cm và \[{\rm{\mu }} = 0,5.\] Ban đầu vật nặng nằm tại vị trí lò xo không biến dạng, truyền cho vật vận tốc ban đầu \({{\rm{v}}_0} = 60{\rm{\pi }}\)cm/s dọc theo trục của lò xo hướng theo chiều lò xo giãn. Lấy g = 10 m/s2. Tốc độ trung bình của vật nặng kể từ thời điểm ban đầu đến khi nó đổi chiều chuyển động lần thứ nhất có giá trị bằng bao nhiêu cm/s? Làm tròn đến phần nguyên.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: \({\rm{k}} = 100\;{\rm{N}}/{\rm{m}};{\rm{m}} = 100\;{\rm{g}},\omega = \sqrt {\frac{{\rm{k}}}{{\rm{m}}}} = \sqrt {\frac{{100}}{{\left( {100 \cdot {{10}^{ - 3}}} \right)}}} = 10\pi {\rm{rad}}/{\rm{s}} \to {\rm{T}} = 0,2\;{\rm{s}}\).
Chuyển động của vật kể từ thời điểm ban đầu đến lúc nó đổi chiều chuyển động lần đầu tiên được chia thành các giai đoạn sau:
Giai đoạn 1: Chuyển động từ O đến C có:
\({{\rm{A}}_1} = \frac{{{{\rm{v}}_0}}}{{\rm{\omega }}} = \frac{{60{\rm{\pi }}}}{{10{\rm{\pi }}}} = 6\;{\rm{cm}},{{\rm{t}}_1} = \frac{{\rm{T}}}{{12}} = \frac{{0,2}}{{12}} = \frac{1}{{60}}\;{\rm{s}},{{\rm{v}}_{\rm{C}}} = \frac{{\sqrt 3 }}{2}{{\rm{v}}_0} = \frac{{\sqrt 3 }}{2}.(60{\rm{\pi }}) = 30\sqrt 3 {\rm{\pi cm}}/{\rm{s}}\).
Giai đoạn 2: Chuyển động từ C đến D là dao động điều hòa chịu thêm tác dụng của ma sát có độ lớn không đổi.
Vị trí cân bằng mới lệch khỏi O theo hướng lò xo bị nén một đoạn
\[\Delta {\ell _0} = \frac{{{\rm{\mu mg}}}}{{\rm{k}}} = \frac{{0,5){{.100.10}^{ - 3}}.10}}{{100}} = 0,5\;{\rm{cm}}\]
\( \to {{\rm{A}}_2} = \sqrt {{{\left( {\Delta {\ell _0} + {\rm{OC}}} \right)}^2} + {{\left( {\frac{{{{\rm{v}}_{\rm{C}}}}}{{\rm{\omega }}}} \right)}^2}} = \sqrt {{{(0,5 + 3)}^2} + {{\left( {\frac{{30\sqrt 3 {\rm{\pi }}}}{{10{\rm{\pi }}}}} \right)}^2}} = 6,265\;{\rm{cm}}\)
\(\Delta {{\rm{t}}_2} = \frac{{\arccos \left( {\frac{{3,5}}{{6,265}}} \right) - \arccos \left( {\frac{{4,5}}{{6,265}}} \right)}}{{{{360}^0}}} \cdot (0,2) = 6,64 \cdot {10^{ - 3}}\;{\rm{s}}\)
\({{\rm{v}}_{\rm{D}}} = {\rm{\omega }}{{\rm{A}}_2}\sqrt {\ell - {{\left( {\frac{{\Delta {\ell _0} + {\rm{OD}}}}{{{{\rm{A}}_2}}}} \right)}^2}} = (10{\rm{\pi }}).(6,265).\sqrt {1 - {{\left( {\frac{{4,5}}{{6,265}}} \right)}^2}} = 136,940\;\)cm/s.
Giai đoạn 3: Chuyển động từ D đến khi đổi chiều lần đầu tiên là dao động điều hòa quanh vị trí lò xo không biến dạng với biên độ
\({{\rm{A}}_3} = \sqrt {{\rm{O}}{{\rm{D}}^2} + {{\left( {\frac{{{{\rm{v}}_{\rm{D}}}}}{\omega }} \right)}^2}} = \sqrt {{4^2} + {{\left( {\frac{{136,940}}{{10\pi }}} \right)}^2}} = 5,916\;{\rm{cm}}\)
\({{\rm{t}}_3} = \frac{{\arccos \left( {\frac{{{\rm{OD}}}}{{{{\rm{A}}_3}}}} \right)}}{{{{360}^0}}}\;{\rm{T}} = \frac{{\arccos \left( {\frac{4}{{5,916}}} \right)}}{{{{360}^0}}} \cdot (0,2) = 0,0264\;{\rm{s}}\)
\({{\rm{v}}_{{\rm{tb}}}} = \frac{{\rm{S}}}{{\rm{t}}} = \frac{{{\rm{OC}} + {\rm{CD}} + \left( {{{\rm{A}}_3} - {\rm{OD}}} \right)}}{{{{\rm{t}}_1} + {{\rm{t}}_2} + {{\rm{t}}_3}}} = \frac{{3 + 1 + (5,916 - 4)}}{{\frac{1}{{60}} + 6,64 \cdot {{10}^{ - 3}} + 0,0264}} = 119,018\)
Đáp án. 119 .
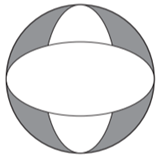
Cho đường tròn có đường kính bằng 4 và 2 Elip lần lượt nhận 2 đường kính vuông góc với nhau của đường tròn làm trục lớn, trục bé của mỗi Elip đều bằng 1. Diện tích \[S\] phần hình phẳng ở bên trong đường tròn và bên ngoài 2 Elip (phần gạch tô màu trên hình vẽ) gần với kết quả nào nhất trong 4 kết quả dưới đây?
Cho hàm số \(f\left( x \right) = 2{x^2} - 4x - 2.\) Gọi \(S\) là tống tất cả các giá trị của tham số \(m\) để hàm số \(y = g\left( x \right) = \left| {{f^2}\left( x \right) - 2f\left( x \right) + m} \right|\) đạt giá trị lớn nhất trên đoạn \(\left[ { - 1\,;\,\,3} \right]\) bằng 15. Tổng \(S\) thuộc khoảng nào sau đây?
Các hình dưới đây biểu diễn dung dịch nước của ba acid \({\rm{HA}}\,({\rm{A}} = {\rm{X}},{\rm{Y}},{\rm{Z}})\); bỏ qua sự phân li của nước.
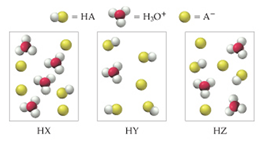
Các dung dịch đều có cùng nồng độ, dung dịch nào dẫn điện tốt nhất?
Cho tập hợp \(A = \left[ {4\,;\,\,7} \right]\) và \(B = \left[ {2a + 3b - 1\,;\,\,3a - b + 5} \right]\) với \(a,\,\,b \in \mathbb{R}.\) Khi \(A = B\) thì giá trị biểu thức \(M = {a^2} + {b^2}\) bằng
Đọc đoạn trích sau và trả lời câu hỏi:
Tỉnh dậy hắn thấy già mà vẫn còn cô độc. Buồn thay cho đời! Có lý nào như thế được? Hắn đã già rồi hay sao? Ngoài bốn mươi tuổi đầu... Dẫu sao, đó không phải tuổi mà người ta mới bắt đầu sửa soạn. Hắn đã tới cái dốc bên kia của đời. Ở những người như hắn, chịu đựng biết bao nhiêu là chất độc, đầy đọa cực nhọc mà chưa bao giờ ốm, một trận ốm có thể gọi là dấu hiệu báo rằng cơ thể đã hư hỏng nhiều. Nó là một cơn mưa gió cuối thu cho biết trời gió rét, nay mùa đông đã đến. Chí Phèo hình như đã trông thấy trước tuổi già của hắn, đói rét và ốm đau, và cô độc, cái này còn đáng sợ hơn đói rét và ốm đau.
(Chí Phèo – Nam Cao)
Biện pháp tu từ nào được sử dụng trong câu “Hắn đã tới cái dốc bên kia của đời”?
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B khác tiếp điểm. Tính độ dài đoạn thẳng AB ?
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _5}\frac{{{x^2} - 4}}{{49}} < {\log _7}\frac{{{x^2} - 4}}{{25}}\)?
Hỗn hợp X gồm ba ester đơn chức đều có công thức phân tử \({{\rm{C}}_8}{{\rm{H}}_8}{{\rm{O}}_2}\); chứa vòng benzene (vòng benzene chỉ có một nhóm thế) và một ester hai chức là ethyl phenyl oxalate. Thủy phân hoàn toàn 7,38 gam X trong lượng dư dung dịch \({\rm{NaOH}}\), thấy có \(0,08\;{\rm{mol}}\,\,{\rm{NaOH}}\) phản ứng, thu được \({\rm{m}}\) gam hỗn hợp muối và 2,18 gam hỗn hợp alcohol Y. Cho toàn bộ Y tác dụng với Na dư, thu được 0,4958 lít khí \({{\rm{H}}_2}\)(đkc). Giá trị của m là
Đáp án: ……….
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)