Một loài thực vật, xét 2 cặp gen phân li độc lập, alen A quy định thân cao trội hoàn toàn so với alen a quy định thân thấp, alen B quy định khả năng chịu mặn trội hoàn toàn so với alen b quy định không có khả năng chịu mặn; cây có kiểu gen bb không có khả năng sống khi trồng trong đất ngập mặn và hạt có kiểu gen bb không nảy mầm trong đất ngập mặn. Để nghiên cứu và ứng dụng trồng rừng phòng hộ ven biển, người ta cho 2 cây (P) dị hợp 2 cặp gen giao phấn với nhau để tạo ra các cây F1 ở vườn ươm không nhiễm mặn; sau đó chọn tất cả các cây thân cao F1 đem trồng ở vùng đất ngập mặn ven biển. Các cây này giao phấn ngẫu nhiên tạo ra F2. Theo thuyết, trong tổng số cây F2 ở vùng đất này, số cây thân cao, chịu mặn chiếm tỉ lệ bao nhiêu?
Đáp án: ……….
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: \({\rm{P}}:{\rm{AaBb}} \times {\rm{AaBb}} \to {{\rm{F}}_1}:(1{\rm{AA}}:2{\rm{Aa}}:1{\rm{aa}}) \times (1{\rm{BB}}:2{\rm{Bb}}:1{\rm{bb}})\).
Chọn các cây thân cao A- đem trồng ở đất ngập mặn (chỉ có các cây B- là sống được) thì tỉ lệ kiểu gen các cây sống được là: (1AA : 2Aa)×(1BB : 2Bb).
Cho các cây F1 sống được giao phấn ngẫu nhiên: (2A : 1a)×(2B : 1b)
→ Tỉ lệ kiểu gen các hạt \({{\rm{F}}_2}\) thu được là: (4AA : 4Aa : 1aa)(4BB : 4Bb : 1bb).
→ Tỉ lệ kiểu gen các cây \({{\rm{F}}_2}\) sống được ở vùng đất mặn này là: (4AA : 4Aa : 1aa)(1BB : 1Bb).
→ Trong số cây \({{\rm{F}}_2}\) sống ở vùng đất này thì cây thân cao chịu mặn A-B- chiếm tỉ lệ là \(\frac{8}{9}.\)
Đáp án: \(\frac{8}{9}.\)
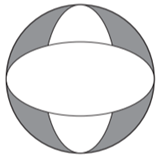
Cho đường tròn có đường kính bằng 4 và 2 Elip lần lượt nhận 2 đường kính vuông góc với nhau của đường tròn làm trục lớn, trục bé của mỗi Elip đều bằng 1. Diện tích \[S\] phần hình phẳng ở bên trong đường tròn và bên ngoài 2 Elip (phần gạch tô màu trên hình vẽ) gần với kết quả nào nhất trong 4 kết quả dưới đây?
Cho hàm số \(f\left( x \right) = 2{x^2} - 4x - 2.\) Gọi \(S\) là tống tất cả các giá trị của tham số \(m\) để hàm số \(y = g\left( x \right) = \left| {{f^2}\left( x \right) - 2f\left( x \right) + m} \right|\) đạt giá trị lớn nhất trên đoạn \(\left[ { - 1\,;\,\,3} \right]\) bằng 15. Tổng \(S\) thuộc khoảng nào sau đây?
Các hình dưới đây biểu diễn dung dịch nước của ba acid \({\rm{HA}}\,({\rm{A}} = {\rm{X}},{\rm{Y}},{\rm{Z}})\); bỏ qua sự phân li của nước.
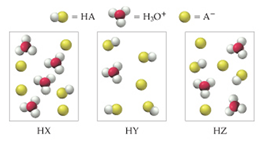
Các dung dịch đều có cùng nồng độ, dung dịch nào dẫn điện tốt nhất?
Cho tập hợp \(A = \left[ {4\,;\,\,7} \right]\) và \(B = \left[ {2a + 3b - 1\,;\,\,3a - b + 5} \right]\) với \(a,\,\,b \in \mathbb{R}.\) Khi \(A = B\) thì giá trị biểu thức \(M = {a^2} + {b^2}\) bằng
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B khác tiếp điểm. Tính độ dài đoạn thẳng AB ?
Hỗn hợp X gồm ba ester đơn chức đều có công thức phân tử \({{\rm{C}}_8}{{\rm{H}}_8}{{\rm{O}}_2}\); chứa vòng benzene (vòng benzene chỉ có một nhóm thế) và một ester hai chức là ethyl phenyl oxalate. Thủy phân hoàn toàn 7,38 gam X trong lượng dư dung dịch \({\rm{NaOH}}\), thấy có \(0,08\;{\rm{mol}}\,\,{\rm{NaOH}}\) phản ứng, thu được \({\rm{m}}\) gam hỗn hợp muối và 2,18 gam hỗn hợp alcohol Y. Cho toàn bộ Y tác dụng với Na dư, thu được 0,4958 lít khí \({{\rm{H}}_2}\)(đkc). Giá trị của m là
Đáp án: ……….
Trên mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình \({d_1}:3x - 4y + 15 = 0,\,\,{d_2}:5x + 2y - 1 = 0\) và \({d_3}:mx - \left( {2m - 1} \right)y + 9m - 13 = 0.\) Tất cả các giá trị của tham số \(m\) để ba đường thẳng đã cho cùng đi qua một điểm là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)