Cho đường tròn tâm \(O\) đường kính \[AB\] và \(M\) là điểm chính giữa của cung \[AB\]. Lấy điểm \(D\) thuộc dây \(MB\,\,\left( D \right.\) khác \(M\) và \(\left. B \right).\) Tia \[AD\] cắt cung nhỏ \[BM\] tại \(N,\) tia \[AM\] cắt tia \[BN\] tại \(C.\)
1) Chứng minh: tứ giác \(CMDN\) nội tiếp được đường tròn.
2) Chứng minh: \(AM \cdot AC = AD \cdot AN.\)
3) Chứng minh: \(\widehat {MCD} = \widehat {OMB}.\)
Giải bởi Vietjack
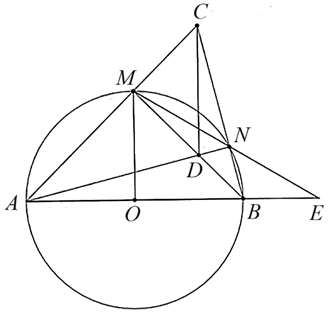
1) Do \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn) nên \(\widehat {CMB} = \widehat {CND} = 90^\circ .\)
Xét tứ giác \[CMDN\] có
\[\widehat {CMD} + \widehat {CND} = 90^\circ + 90^\circ = 180^\circ .\]
Mà hai góc này ở vị trí đối diện nên tứ giác \[CMDN\] nội tiếp được trong đường tròn.
2) Xét \(\Delta AMD\) và \(\Delta ANC\) có \(\widehat {NAC}\) chung; \(\widehat {AMD} = \widehat {ANC} = 90^\circ .\)
Do đó , suy ra \(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}}\) hay \(AM \cdot AC = AN \cdot AD\).
3) Do \[ABNM\] nội tiếp \(\left( O \right)\) nên \(\widehat {BAM} + \widehat {BNM} = 180^\circ \).
Mà \(\widehat {BNM} + \widehat {CNM} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CNM} = \widehat {BAM}\).
Mà \[\widehat {CNM} = \widehat {MCD}\] (góc nội tiếp cùng chắn cung
Suy ra \(\widehat {MCD} = \widehat {OMB}\,\,\left( { = \widehat {CNM}} \right)\) hay \(\widehat {MCD} = \widehat {OMB}.\)
4) Do \[M\] là điểm chính giữa cung \[AB\] nên \(MA = MB\).
Suy ra \(\widehat {MNA} = \widehat {MAB}\) (góc nội tiếp chắn hai cung bằng nhau).
Xét \(\Delta MAN\) và \(\Delta MAE\) có \(\widehat {AME}\) chung; \(\widehat {MNA} = \widehat {MAE}\,\,({\rm{cmt}})\).
Do đó .
Suy ra \(\widehat {MAN} = \widehat {MEA}\) (hai góc tương ứng).
Mà \[\widehat {MAN} = \widehat {MBN}\] (góc nội tiếp cùng chắn nên \(\widehat {MBN} = \widehat {MEB}\).
Do đó \(\widehat {DBN} = \widehat {NEB}\) (đpcm).
Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
1) Giải phương trình, hệ phương trình sau:
a) \({x^4} - 8{x^2} - 9 = 0\). b) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 9}\\{3x - 2y = - 3}\end{array}} \right.\).
Cho Parabol \(\left( P \right):y = \frac{3}{4}{x^2}\) và đường thẳng \(\left( d \right):y = x + m\) với \(m\) là tham số.
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\).
Cho phương trình: \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0\). (\(m\) là tham số).
1) Tìm các giá trị của tham số \(m\) để phương trình đã cho có nghiệm bằng 2.
