Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Bình Dương 2024 - 2025 (Đề 15)
-
72 lượt thi
-
5 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
1) Giải phương trình, hệ phương trình sau:
a) \({x^4} - 8{x^2} - 9 = 0\). b) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 9}\\{3x - 2y = - 3}\end{array}} \right.\).
 Xem đáp án
Xem đáp án
1) a) \({x^4} - 8{x^2} - 9 = 0\). Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\). Phương trình đã cho trở thành \({t^2} - 8t - 9 = 0.\)
Ta thấy \(1 - \left( { - 8} \right) + \left( { - 9} \right) = 0\) nên phương trình có 2 nghiệm \(t = - 1\) (loại) hoặc \(t = 9\,\,\left( {{\rm{TM}}} \right).\)
Với \(t = 9\) thì \({x^2} = 9\). Do đó \(x = 3\) hoặc \(x = - 3.\)
Vậy phương trình đã cho có nghiệm \[x = - 3\,;\,\,x = 3.\]
b) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 9}\\{3x - 2y = - 3}\end{array}} \right.\). Nhân hai vế của phương trình thứ nhất với 2, ta được hệ: \(\left\{ {\begin{array}{*{20}{l}}{2x + 2y = 18}\\{3x - 2y = - 3}\end{array}} \right..\)
Cộng từng vế của phương trình mới, ta được: \[5x = 15\], tức là \[x = 3.\]
Thế \[x = 3\] vào phương trình \[x + y = 9\] ta có: \[3 + y = 9\] hay \[y = 6\].
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x\,;\,\,y} \right) = \left( {3\,;\,\,6} \right)\).
2) \(M = 2\sqrt {9 - 4\sqrt 5 } - \sqrt {20} = 2\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} - \sqrt {4 \cdot 5} \)\( = 2\left| {\sqrt 5 - 2} \right| - 2\sqrt 5 = 2\sqrt 5 - 4 - 2\sqrt 5 = - 4\).
Vậy \(M = 2\sqrt {9 - 4\sqrt 5 } = - 4\).
Câu 2:
Cho Parabol \(\left( P \right):y = \frac{3}{4}{x^2}\) và đường thẳng \(\left( d \right):y = x + m\) với \(m\) là tham số.
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\).
 Xem đáp án
Xem đáp án
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\).
Tập xác định \(D = \mathbb{R}\).
Bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = \frac{3}{4}{x^2}\) |
3 |
\(\frac{3}{4}\) |
0 |
\(\frac{3}{4}\) |
3 |
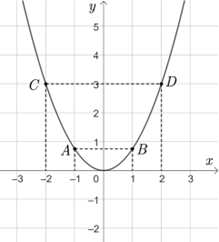
2) Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình:
\(\frac{3}{4}{x^2} = x + m\) hay \(\frac{3}{4}{x^2} - x - m = 0\).
Để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình trên phải có hai nghiệm phân biệt
Hay \(\Delta = {( - 1)^2} - 4 \cdot \frac{3}{4}( - m) = 1 + 3m > 0\) hay \(m > \frac{{ - 1}}{3}\).
Vậy với \(m > \frac{{ - 1}}{3}\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Câu 3:
Cho phương trình: \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0\). (\(m\) là tham số).
1) Tìm các giá trị của tham số \(m\) để phương trình đã cho có nghiệm bằng 2.
 Xem đáp án
Xem đáp án
1) Để phương trình có nghiệm bằng 2, thay \(x = 2\) vào phương trình, ta được:
\({2^2} - 2\left( {m - 2} \right) \cdot 2 + {m^2} - 8 = 0\) hay \(4 - 4m + 8 + {m^2} - 8 = 0\).
Khi đó \({m^2} - 4m + 4 = 0\) hay \({\left( {m - 2} \right)^2} = 0\) nên \(m = 2\).
Vậy \(m = 2\) thì phương trình có nghiệm \(x = 2\)
2) \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0 & \left( 1 \right)\)
Ta có \[\Delta = 4{\left( {m - 2} \right)^2} - 4\left( {{m^2} - 8} \right) = 4{m^2} - 16m + 16 - 4{m^2} + 32 = - 32m + 48\].
Để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt thì \[\Delta > 0\] hay \[ - 32m + 48 > 0\] nên \[m < 3.\]
Khi đó \(\left( 1 \right)\) có hai nghiệm phân biệt \[{x_1},{\rm{ }}{x_2}.\]
Áp dụng hệ thức Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 2} \right)}\\{{x_1}{x_2} = {m^2} - 8}\end{array}} \right.\).
Để \(4{x_1} - 3{x_2} = 25\) thì \(\left\{ {\begin{array}{*{20}{l}}{4{x_1} - 3{x_2} = 25}\\{{x_1} + {x_2} = 2m - 4\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\).
Nhân hai vế của phương trình \[\left( 2 \right)\] với 4, ta được hệ: \(\left\{ {\begin{array}{*{20}{l}}{4{x_1} - 3{x_2} = 25 & & \left( 3 \right)}\\{4{x_1} + 4{x_2} = 8m - 16 & \left( 4 \right)}\end{array}} \right..\)
Trừ từng vế phương trình \(\left( 4 \right)\) cho \(\left( 3 \right)\) ta được: \(7{x_2} = 8m - 41\), tức là \({x_2} = \frac{{8m - 41}}{7}.\)
Thế \({x_2} = \frac{{8m - 41}}{7}\) vào phương trình \[\left( 2 \right)\] ta có: \({x_1} + \frac{{8m - 41}}{7} = 2m - 4\) hay \({x_1} = \frac{{6m + 13}}{7}.\)
Thay \({x_1} = \frac{{6m + 13}}{7}\,;\,\,{x_2} = \frac{{8m - 41}}{7}\) vào \({x_1}{x_2} = {m^2} - 8\) ta được
\(\frac{{6m + 13}}{7} \cdot \frac{{8m - 41}}{7} = {m^2} - 8\)
\(\frac{{\left( {6m + 13} \right)\left( {8m - 41} \right)}}{{49}} = {m^2} - 8\)
\[\left( {6m + 13} \right)\left( {8m - 41} \right) = 49\left( {{m^2} - 8} \right)\]
\(48{m^2} - 142m - 533 = 49{m^2} - 392\)
\({m^2} + 142m + 141 = 0\).
Ta thấy \(1 - 142 + 141 = 0\) nên phương trình có nghiệm \(m = - 1\) hoặc \(m = - 141\) (thỏa mãn \(m < 3).\)
Vậy \[m \in \left\{ { - 1\,;\,\, - 141} \right\}\] thì phương trình đã cho có hai nghiệm phân biệt \({x_1}\), \({x_2}\) thỏa mãn điều kiện \(4{x_1} - 3{x_2} = 25.\)
Câu 4:
Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
 Xem đáp án
Xem đáp án
Gọi \[x\,\,\left( {\rm{m}} \right)\] là chiều dài ban đầu của khu vườn hình chữ nhật \[\left( {0 < x < 100} \right)\].
Khi đó nửa chu vi khu vườn hình chữ nhật là: \(200:2 = 100\,\,\left( m \right).\)
Chiều rộng ban đầu của khu vườn là \(100 - x\,\,\left( {\rm{m}} \right)\).
Chiều dài khu vườn sau khi giảm \(8\,\,{\rm{m}}\) là \(x - 8\,\,\left( {\rm{m}} \right)\).
Diện tích của khu vườn sau khi giảm là: \[\left( {x - 8} \right)\left( {100 - x} \right) = 2\,\,080\]
\[ - {x^2} + 108x - 800 = 2\,\,080\]
\[{x^2} - 108x + 2\,\,880 = 0\]
\(x = 60\) hoặc \(x = 48\).
• Với \(x = 60\) hay chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) thì
Chiều rộng ban đầu của khu vườn là \(100 - 60 = 40\,\,\left( {\rm{m}} \right)\) (thỏa mãn).
• Với \(x = 48\) hay chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) thì
Chiều rộng ban đầu của khu vườn là \(100 - 48 = 52\,\,\left( {\rm{m}} \right)\) (loại vì chiều dài phải lớn hơn chiều rộng).
Vậy chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) và chiều rộng ban đầu của khu vườn là \(40\,\,{\rm{m}}{\rm{.}}\)
Câu 5:
Cho đường tròn tâm \(O\) đường kính \[AB\] và \(M\) là điểm chính giữa của cung \[AB\]. Lấy điểm \(D\) thuộc dây \(MB\,\,\left( D \right.\) khác \(M\) và \(\left. B \right).\) Tia \[AD\] cắt cung nhỏ \[BM\] tại \(N,\) tia \[AM\] cắt tia \[BN\] tại \(C.\)
1) Chứng minh: tứ giác \(CMDN\) nội tiếp được đường tròn.
2) Chứng minh: \(AM \cdot AC = AD \cdot AN.\)
3) Chứng minh: \(\widehat {MCD} = \widehat {OMB}.\)
 Xem đáp án
Xem đáp án
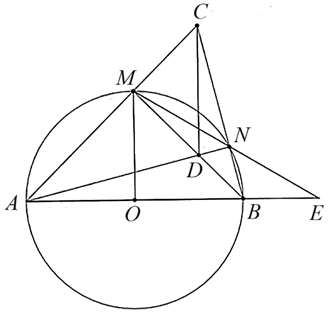
1) Do \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn) nên \(\widehat {CMB} = \widehat {CND} = 90^\circ .\)
Xét tứ giác \[CMDN\] có
\[\widehat {CMD} + \widehat {CND} = 90^\circ + 90^\circ = 180^\circ .\]
Mà hai góc này ở vị trí đối diện nên tứ giác \[CMDN\] nội tiếp được trong đường tròn.
2) Xét \(\Delta AMD\) và \(\Delta ANC\) có \(\widehat {NAC}\) chung; \(\widehat {AMD} = \widehat {ANC} = 90^\circ .\)
Do đó , suy ra \(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}}\) hay \(AM \cdot AC = AN \cdot AD\).
3) Do \[ABNM\] nội tiếp \(\left( O \right)\) nên \(\widehat {BAM} + \widehat {BNM} = 180^\circ \).
Mà \(\widehat {BNM} + \widehat {CNM} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CNM} = \widehat {BAM}\).
Mà \[\widehat {CNM} = \widehat {MCD}\] (góc nội tiếp cùng chắn cung
Suy ra \(\widehat {MCD} = \widehat {OMB}\,\,\left( { = \widehat {CNM}} \right)\) hay \(\widehat {MCD} = \widehat {OMB}.\)
4) Do \[M\] là điểm chính giữa cung \[AB\] nên \(MA = MB\).
Suy ra \(\widehat {MNA} = \widehat {MAB}\) (góc nội tiếp chắn hai cung bằng nhau).
Xét \(\Delta MAN\) và \(\Delta MAE\) có \(\widehat {AME}\) chung; \(\widehat {MNA} = \widehat {MAE}\,\,({\rm{cmt}})\).
Do đó .
Suy ra \(\widehat {MAN} = \widehat {MEA}\) (hai góc tương ứng).
Mà \[\widehat {MAN} = \widehat {MBN}\] (góc nội tiếp cùng chắn nên \(\widehat {MBN} = \widehat {MEB}\).
Do đó \(\widehat {DBN} = \widehat {NEB}\) (đpcm).
