Giải bởi Vietjack
Giải bởi Vietjack
\(f(b) - f(a) = \int_a^b {{f^\prime }} (x)dx = \int_a^c {{f^\prime }} (x)dx + \int_c^b {{f^\prime }} (x)dx = {S_1} - {S_2}.\) Chọn B.
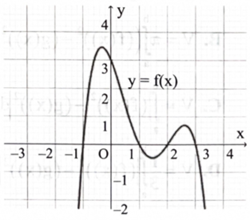
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) có đồ thị cắt trục Ox tại đúng 4 điểm phân biệt (hình bên). Biết rằng \(\int_{ - 1}^1 {\rm{f}} ({\rm{x}}){\rm{dx}} = 21\), \(\int_1^2 f (x)dx = - 2,\int_2^3 f (x)dx = 3.\) Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và trục Ox bằng
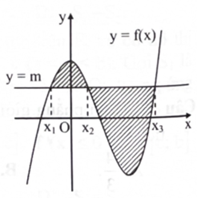
Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1},{{\rm{x}}_2},{{\rm{x}}_3}\) \(\left( {{x_1} < {x_2} < {x_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành là
![Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1},{{\rm{x}}_2},{{\rm{x}}_3}\) \(\left( {{x_1} < {x_2} < {x_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành là A. \(\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx.\) B. \(\int_{{x_1}}^{{x_2}} f (x)dx - \int_{{x_2}}^{{x_3}} f (x)dx.\) C. \[\left| {\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx} \right|.\] D. \(\left| {\int_{{{\rm{x}}_1}}^{{{\rm{x}}_3}} {\rm{f}} ({\rm{x}}){\rm{dx}}} \right|.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid3-1727016691.png)
Hình vẽ bên biểu diễn đường thẳng\({\rm{y}} = {\rm{m}}\)cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1}\), \({{\rm{x}}_2},{{\rm{x}}_3}\left( {{{\rm{x}}_1} < {{\rm{x}}_2} < {{\rm{x}}_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi hai đường trên là
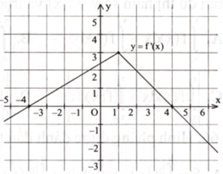
Cho hàm số \(y = f(x)\) thoả mãn hàm \(y = {f^\prime }(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị của biểu thức \({\rm{f}}(4) - {\rm{f}}( - 4)\) bằng
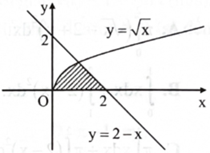
Diện tích hình phẳng giới hạn bởi các đường \({\rm{y}} = \sqrt {\rm{x}} ,{\rm{y}} = 2 - {\rm{x}}\) và trục Ox được tính bởi công thức
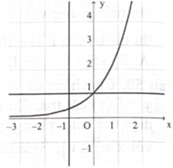
Hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{e}}^{\rm{x}}}\) và các đường thẳng \({\rm{y}} = 1,{\rm{x}} = - 1\) có diện tích là