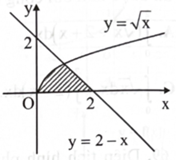
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường \({\rm{y}} = \sqrt {\rm{x}} ,{\rm{y}} = 2 - {\rm{x}}\) và trục hoành quay xung quanh Ox được tính bởi công thức
Giải bởi Vietjack
\(\sqrt x = 2 - x \Leftrightarrow x = 1.V = {V_1} + {V_2}.\)
V1 là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0,x = 1\) quay quanh trục Ox.
V2 là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường \(y = 2 - x,y = 0,x = 1\) quay quanh trục Ox.
\({\rm{V}} = \pi \int_0^1 {{\rm{xdx}}} + \pi \int_1^2 {{{(2 - {\rm{x}})}^2}} {\rm{dx}}.\) Chọn C.
Thể tích khối tròn xoay khi quay hình phẳng D trong hình vẽ xung quanh trục Ox được tính bởi công thức
Cho \({\rm{a}} > {\rm{b}} > 0.\) Thể tích khối tròn xoay tạo thành khi cho elip \(\frac{{{{\rm{x}}^2}}}{{{{\rm{a}}^2}}} + \frac{{{{\rm{y}}^2}}}{{\;{{\rm{b}}^2}}} = 1\) quay xung quanh trục Ox là
