4 câu hỏi trắc nghiệm thuộc DẠNG 4. MỐI LIÊN HỆ GIỮA TÍCH PHÂN VÀ THỂ TÍCH CỦA VẬT THỂ

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 2: Nguyên hàm, tích phân và ứng dụng có đáp án

DẠNG 4. MỐI LIÊN HỆ GIỮA TÍCH PHÂN VÀ THỂ TÍCH CỦA VẬT THỂ

78 lượt thi
4 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Cho hàm số $y = f(x)$ liên tục trên $[a;b](a,b \in \mathbb{R},a < b).$ Gọi $D$ là hình phẳng giới hạn bởi các đường ${\rm{y}} = {\rm{f}}({\rm{x}}),{\rm{x}} = {\rm{a}},{\rm{x}} = {\rm{b}}$ và trục hoành. Quay hình phẳng D quanh trục Ox ta được một khối tròn xoay có thể tích được tính bởi công thức

A. ${\rm{V}} = \int_{\rm{a}}^{\rm{b}} {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.$

B. $V = \pi \int_b^a {(f(} x){)^2}dx.$

C. $V = \frac{1}{3}\pi \int_{\rm{a}}^{\rm{b}} {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.$

D. $V = \pi \int_a^b {(f(} x){)^2}dx.$

Xem đáp án

Chọn đáp án D

Câu 2:

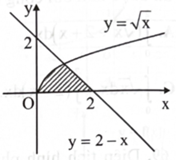
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường ${\rm{y}} = \sqrt {\rm{x}} ,{\rm{y}} = 2 - {\rm{x}}$ và trục hoành quay xung quanh Ox được tính bởi công thức

$Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường ${\rm{y}} = \sqrt {\rm{x}} ,{\rm{y}} = 2 - {\rm{x}}$ và trục hoành quay xung quanh Ox được tính bởi công thức (ảnh 1)$

A. $\pi \int_0^2 {{{(\sqrt x - 2 + x)}^2}} dx.$

B. $\int_0^1 x dx + \int_1^2 {{{(2 - x)}^2}} dx.$

C. $\pi \int_0^1 x dx + \pi \int_1^2 {{{(2 - x)}^2}} dx.$

D. $\pi \int_0^2 x dx + \pi \int_0^2 {{{(2 - x)}^2}} dx.$

Xem đáp án

$\sqrt x = 2 - x \Leftrightarrow x = 1.V = {V_1} + {V_2}.$

V₁ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = \sqrt x ,y = 0,x = 1$ quay quanh trục Ox.

V₂ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = 2 - x,y = 0,x = 1$ quay quanh trục Ox.

${\rm{V}} = \pi \int_0^1 {{\rm{xdx}}} + \pi \int_1^2 {{{(2 - {\rm{x}})}^2}} {\rm{dx}}.$ Chọn C.

Câu 3:

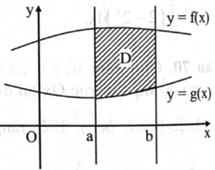
Thể tích khối tròn xoay khi quay hình phẳng D trong hình vẽ xung quanh trục Ox được tính bởi công thức

A. $V = \frac{1}{3}\pi \int_a^b {\left| {{{(f(x))}^2} - {{(g(x))}^2}} \right|} dx.$

B. $V = \pi \int_a^b {\left( {{{(f(x))}^2} - {{(g(x))}^2}} \right)} dx.$

C. $V = \int_a^b {\left| {{{(f(x))}^2} - {{(g(x))}^2}} \right|} dx.$

D. $V = \frac{1}{3}\int_a^b {\left| {{{(f(x))}^2} - {{(g(x))}^2}} \right|} dx.$

Xem đáp án

$V = {V_1} - {V_2}.$

V₁ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường ${\rm{y}} = {\rm{f}}({\rm{x}}),{\rm{x}} = {\rm{a}},{\rm{x}} = {\rm{b}}$ quay quanh trục Ox.

V₂ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường ${\rm{y}} = {\rm{g}}({\rm{x}}),{\rm{x}} = {\rm{a}},{\rm{x}} = {\rm{b}}$ quay quanh trục $O{\rm{x}}.$

${\rm{V}} = \pi \int_{\rm{a}}^{\rm{b}} {\left( {{{({\rm{f}}({\rm{x}}))}^2} - {{({\rm{g}}({\rm{x}}))}^2}} \right)} {\rm{dx}}.$ Chọn B.

Câu 4:

Cho ${\rm{a}} > {\rm{b}} > 0.$ Thể tích khối tròn xoay tạo thành khi cho elip $\frac{{{{\rm{x}}^2}}}{{{{\rm{a}}^2}}} + \frac{{{{\rm{y}}^2}}}{{\;{{\rm{b}}^2}}} = 1$ quay xung quanh trục Ox là

A. $\frac{4}{3}\pi {{\rm{a}}^2}\;{\rm{b}}.$

B. $\frac{4}{3}\pi {\rm{a}}{{\rm{b}}^2}.$

C. $\frac{1}{3}\pi {{\rm{a}}^2}\;{\rm{b}}.$

D. $\frac{1}{3}\pi {\rm{a}}{{\rm{b}}^2}.$

Xem đáp án

$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Leftrightarrow {y^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) \Leftrightarrow y = \pm b\sqrt {1 - \frac{{{x^2}}}{{{a^2}}}} ,x \in [ - a;a].$

Nhận xét: Elip nhận ${\rm{Ox}},{\rm{Oy}}$ là hai trục đối xứng.

Ta cần tính thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường

$y = b\sqrt {1 - \frac{{{x^2}}}{{{a^2}}}} ,x = - a,x = a$quay quanh trục Ox.

$V = \pi \int_{ - a}^a {{{\left( {b\sqrt {1 - \frac{{{x^2}}}{{{a^2}}}} } \right)}^2}} dx = \pi \int_{ - a}^a {{b^2}} \left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)dx = \left. {\pi {b^2}\left( {x - \frac{{{x^3}}}{{3{a^2}}}} \right)} \right|_{ - a}^a = \frac{{4\pi }}{3}a{b^2}$

Chọn B.

Bắt đầu thi ngay