(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 4)
-
171 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R})\) ở hình bên có đường tiệm cận xiên là một trong bốn đường thẳng dưới đây, đường thẳng đó là đường nào?
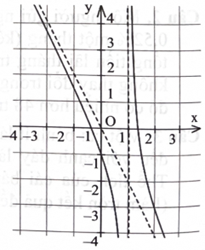
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 2:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 3:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 4:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 8:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 10:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 12:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 13:
c) Chiều cao của khối bê tông là 4 cm.
 Xem đáp án
Xem đáp án
c) Chiều cao của khối bê tông là 4 dm.
=> Sai
Câu 14:
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về cân nặng của một số quả bưởi da xanh ở một khu vực (đơn vị: kg).
|
Nhóm |
[1,2 ; 1,3) |
[1,3 ; 1,4) |
[1,4 ; 1,5) |
[1,5 ; 1,6) |
[1,6 ; 1,7) |
|
Tần số |
8 |
21 |
8 |
7 |
6 |
Số trung bình của mẫu số liệu ghép nhóm trên là bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)
 Xem đáp án
Xem đáp án
Đáp số: 1,41.
\(\overline {\rm{x}} = \frac{{8 \cdot 1,25 + 21 \cdot 1,35 + 8 \cdot 1,45 + 7 \cdot 1,55 + 6 \cdot 1,65}}{{50}} \approx 1,41\)
Câu 15:
Hai bạn Việt và Nam mỗi người thực hiện một thí nghiệm một cách độc lập với nhau. Xác suất thực hiện thành công thí nghiệm của Việt và Nam lẩn lượt là 0,6 và 0,7. Xác suất có đúng một trong hai người thực hiện thành công thí nghiệm biết rằng có ít nhất một người thực hiện thành công thí nghiệm là \(\frac{{\rm{a}}}{{\rm{b}}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{N},{\rm{b}} < 50.\) Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp số: 67.
Gọi V là biến cố bạn Việt thực hiện thành công thí nghiệm; N là biến cố bạn Nam thực hiện thành công thí nghiệm. Ta có \({\rm{P}}({\rm{V}}) = 0,6;{\rm{P}}({\rm{N}}) = 0,7.\)
\({\rm{V}} \cup {\rm{N}}\) là biến cố có ít nhất một người thực hiện thành công thí nghiệm và \(\overline {\rm{V}} {\rm{N}} \cup {\rm{VN}}\) là biến cố có đúng một người thực hiện thành công thí nghiệm.
Ta có \({\rm{P}}({\rm{V}} \cup {\rm{N}}) = 0,6 + 0,7 - 0,6 \cdot 0,7 = 0,88\)
và \(P(\overline {\rm{V}} N \cup N\overline {\rm{V}} ) = {\rm{P}}(\overline {\rm{V}} N) + {\rm{P}}({\rm{N}}\overline {\rm{V}} ) = 0,4 \cdot 0,7 + 0,6 \cdot 0,3 = 0,46.\)
Xác suất cần tính là \(P(\overline {\rm{V}} N \cup N\overline {\rm{V}} \mid {\rm{V}} \cup {\rm{N}}) = \frac{{{\rm{P}}(\overline {\rm{V}} N \cup N\overline {\rm{V}} )}}{{{\rm{P}}({\rm{V}} \cup {\rm{N}})}} = \frac{{23}}{{44}}.\)
\(a + b = 23 + 44 = 67\)
