Giải bởi Vietjack
Đáp án đúng là: C
⦁ Thay \[x = 1,y = - 5\] vào phương trình \[x - 5y = 13,\] ta được: \[1 - 5 \cdot \left( { - 5} \right) = 26 \ne 13.\]
Do đó cặp số \[\left( {1; - 5} \right)\] không là nghiệm của hệ phương trình ở các phương án A, B.
⦁ Thay \[x = 1,y = - 5\] vào mỗi phương trình trong hệ ở phương án C, ta được:
\[1 - \left( { - 5} \right) = 6\] (đúng);
\[2 \cdot 1 + \left( { - 5} \right) = - 3\] (đúng).
Do đó cặp số \[\left( {1; - 5} \right)\] là nghiệm của từng phương trình trong hệ phương trình ở phương án C.
Vì vậy cặp số \[\left( {1; - 5} \right)\] là nghiệm của hệ phương trình ở phương án C.
⦁ Thay \[x = 1,y = - 5\] vào phương trình \[x + y = 8,\] ta được: \[1 + \left( { - 5} \right) = - 4 \ne 8\]
Do đó cặp số \[\left( {1; - 5} \right)\] không là nghiệm của hệ phương trình ở phương án D.
Vậy ta chọn phương án C.
III. Vận dụng
I. Nhân biết
II. Thông hiểu
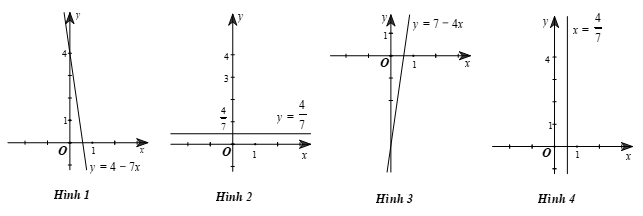
Mỗi nghiệm của phương trình \[7x + 0y = 4\] được biểu diễn bởi một điểm nằm trên đường thẳng có đồ thị là hình vẽ nào trong các hình vẽ sau?
Cho hệ phương trình \[\left\{ \begin{array}{l} - x - 3y = 2\\5x + 9y = - 11\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp thế (biểu diễn \(x\) theo \(y)\), ta được phương trình ẩn \(y\) là
Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím:
