 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Xét phương trình \(\left\{ \begin{array}{l}x - my = 1\,\,\,\,\left( 1 \right)\\mx + y = 3\,\,\,\left( 2 \right)\end{array} \right.\)
Từ phương trình (1), ta có: \(x = my + 1.\,\,\,\left( 3 \right)\)
Thế phương trình (3) vào phương trình (2), ta được:
\(m\left( {my + 1} \right) + y = 3\)
\({m^2}y + m + y = 3\)
\(\left( {{m^2} + 1} \right)y = 3 - m\)
\(y = \frac{{3 - m}}{{{m^2} + 1}}\) (do \({m^2} + 1 \ne 0)\)
Thay \(y = \frac{{3 - m}}{{{m^2} + 1}}\) vào phương trình (3), ta được:
\(x = m \cdot \frac{{3 - m}}{{{m^2} + 1}} + 1 = \frac{{3m - {m^2} + {m^2} + 1}}{{{m^2} + 1}} = \frac{{3m + 1}}{{{m^2} + 1}}.\)
Như vậy, hệ phương trình đã cho có nghiệm là \(\left( {{x_0};\,\,{y_0}} \right) = \left( {\frac{{3m + 1}}{{{m^2} + 1}};\,\,\frac{{3 - m}}{{{m^2} + 1}}} \right)\).
Ta có: \(P = x_0^2 + y_0^2 - {x_0} - 3{y_0} = {\left( {\frac{{3m + 1}}{{{m^2} + 1}}} \right)^2} + {\left( {\frac{{3 - m}}{{{m^2} + 1}}} \right)^2} - \frac{{3m + 1}}{{{m^2} + 1}} - 3 \cdot \frac{{3 - m}}{{{m^2} + 1}}\)
\[ = \frac{{{{\left( {3m + 1} \right)}^2} + {{\left( {3 - m} \right)}^2} - \left( {3m + 1} \right)\left( {{m^2} + 1} \right) - 3\left( {3 - m} \right)\left( {{m^2} + 1} \right)}}{{{{\left( {{m^2} + 1} \right)}^2}}}\]
\[ = \frac{{9{m^2} + 6m + 1 + 9 - 6m + {m^2} - \left( {3{m^3} + 3m + {m^2} + 1} \right) - \left( {9{m^2} + 9 - 3{m^3} - 3m} \right)}}{{{{\left( {{m^2} + 1} \right)}^2}}}\]
\[ = \frac{{9{m^2} + 6m + 1 + 9 - 6m + {m^2} - 3{m^3} - 3m - {m^2} - 1 - 9{m^2} - 9 + 3{m^3} + 3m}}{{{{\left( {{m^2} + 1} \right)}^2}}}\]
\[ = \frac{0}{{{{\left( {{m^2} + 1} \right)}^2}}} = 0.\]
Vậy \(P = 0,\) ta chọn phương án B.
I. Nhân biết
II. Thông hiểu
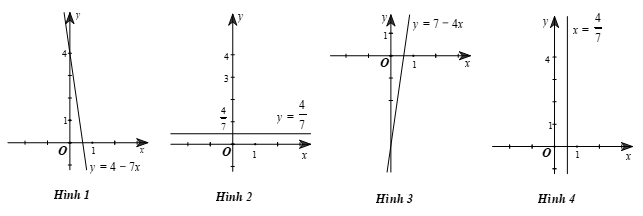
Mỗi nghiệm của phương trình \[7x + 0y = 4\] được biểu diễn bởi một điểm nằm trên đường thẳng có đồ thị là hình vẽ nào trong các hình vẽ sau?
Cho hệ phương trình \[\left\{ \begin{array}{l} - x - 3y = 2\\5x + 9y = - 11\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp thế (biểu diễn \(x\) theo \(y)\), ta được phương trình ẩn \(y\) là
III. Vận dụng
Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím: