Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 16{\rm{\;cm}},\,\,\sin B = \frac{3}{5}.\] Kết quả nào sau đây là sai?
A. \(\cos C = \frac{3}{5}.\)
B. \(\cos B = \frac{4}{5}.\)
C. \[BC = 26,6\] cm.
D. \[AB = 21,3\] cm.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C

Xét tam giác \[ABC\] vuông tại \[A\], có:
⦁ \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) nên \[\cos C = \sin B = \frac{3}{5}.\] Do đó phương án A là khẳng định đúng.
⦁ \[\sin B = \frac{{AC}}{{BC}}.\] Suy ra \[BC = \frac{{AC}}{{\sin B}} = \frac{{16}}{{\frac{3}{5}}} = \frac{{80}}{3} \approx 26,7\] (cm). Do đó phương án C là khẳng định sai.
⦁ \[B{C^2} = A{B^2} + A{C^2}\] (theo định lí Pythagore)
Suy ra \[A{B^2} = B{C^2} - A{C^2} = {\left( {\frac{{80}}{3}} \right)^2} - {16^2} = \frac{{4096}}{9}.\] Do đó \[AB = \frac{{64}}{3} \approx 21,3\] (cm).
Như vậy phương án D là khẳng định đúng.
⦁ \(\cos B = \frac{{AB}}{{BC}} = \frac{{\frac{{64}}{3}}}{{\frac{{80}}{3}}} = \frac{4}{5}.\) Do đó phương án B là khẳng định đúng.
Vậy ta chọn phương án C.
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (hình vẽ), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1{\rm{\;\;}}225\] m và dùng giác kế ngắm xác định được \[\widehat {ABC} = 75^\circ ;\,\,\widehat {ACB} = 65^\circ .\]

Khi đó khoảng cách \[AC\] khoảng bao nhiêu mét?
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với mặt đất một góc bằng \[55^\circ ,\] bóng của một cây xanh trên mặt đất dài \[14,25\] m (như hình vẽ).
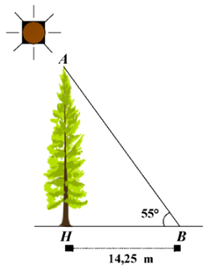
Chiều cao \[AH\] của cây xanh (làm tròn đến hàng phần trăm) là
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng
Một khúc sông rộng khoảng \[250\] m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng \[320\] m mới sang được bờ bên kia. Giả sử dòng nước đã đẩy con đò đi lệch một góc \[\alpha \] (hình vẽ).
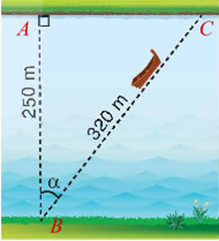
Khi đó để tính giá trị của \[\alpha \], cách đơn giản nhất là sử dụng tỉ số lượng giác nào của góc nhọn \[\alpha \]?
Một cái thang dài \[4,8\] m dựa vào tường và tạo với tường một góc \[32^\circ .\]
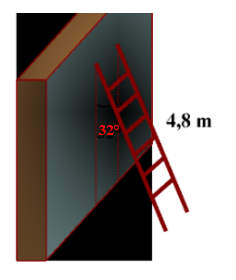
Chiều cao của thang so với mặt đất gần nhất với
III. Vận dụng
Cho tam giác \[ABC\] có \[BC = 9{\rm{\;cm}},\,\,\widehat {ABC} = 50^\circ \] và \[\widehat {ACB} = 35^\circ .\] Gọi \[N\] là chân đường vuông góc hạ từ \[A\] xuống cạnh \[BC.\] Độ dài \[AN\] gần nhất với giá trị nào dưới đây?
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với phương ngang một góc bằng \[35^\circ ,\] khi đó cột \[AH\] có bóng trên mặt đất là đoạn \[BH\] dài \[10,4\] m.
![Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với phương ngang một góc bằng \[35^\circ ,\] khi đó cột \[AH\] có bóng trên mặt đất là đoạn \[BH\] dài \[10,4\] m.Trong các hệ thức sau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1728658068.png)
Trong các hệ thức sau, hệ thức nào là đúng?
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 10{\rm{\;cm}},\,\,\widehat C = 30^\circ .\] Độ dài cạnh \[AB\] bằng
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 12{\rm{\;cm}},\,\,\widehat B = 40^\circ .\] Kết quả nào sau đây là đúng?
Cho hình thang \[ABCD\] có \[\widehat {A\,} = \widehat {D\,} = 90^\circ ,\,\,\widehat {C\,} = 50^\circ .\] Biết rằng \[AB = 2;\,\,AD = 1,2.\] Khi đó diện tích hình thang \[ABCD\] gần nhất với
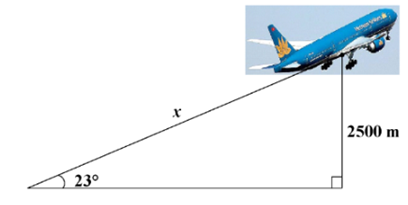
Một máy bay cất cánh theo phương hợp với mặt đất một góc \[23^\circ .\] Hỏi muốn đạt độ cao \[2\,\,500\] m thì máy bay phải bay một đoạn đường \[x\] dài khoảng bao nhiêu mét?