Cho đường thẳng \(\left( d \right):\,\,y = 2x + m\) và parabol \(\left( P \right):\,\,y = {x^2}\,,\) số nguyên \(m\) nhỏ nhất để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt là
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là nghiệm của phương trình
\({x^2} = 2x + m\) hay \({x^2} - 2x + m = 0\,\,\,\left( 1 \right).\)
Ta có: \(\Delta ' = 1 + m\).
Để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt.
Suy ra \(\Delta ' > 0\) hay \(1 + m > 0\) hay \(m > - 1.\)
Mà \(m\) là số nguyên nhỏ nhất nên \(m = 0.\)
Trong mặt phẳng tọa độ \(Oxy,\) biết điểm có hoành độ bằng 1 là một điểm chung của parabol \(y = 2{x^2}\) và đường thẳng \(y = \left( {m - 1} \right)x - 2,\) với \(m\) là tham số. Khi đó giá trị của \(m.\)
Khoảng cách giữa hai điểm \(M\left( {{x_1};\,\,{y_1}} \right)\) và \(N\left( {{x_2};\,\,{y_2}} \right)\) được tính công thức:
\(MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} .\)
Áp dụng: Cho parabol \(\left( P \right):\,\,y = \frac{1}{2}{x^2}\) cắt đường thẳng \(\left( d \right):\,\,y = x + \frac{3}{2}\) tại hai điểm phân biệt \(A\) và \(B.\) Độ dài đoạn thẳng \(AB\) bằng
I. Nhận biết
Kết luận nào sau đây là sai khi nói về đồ thị hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)?\)
Cho đồ thị của một hàm số bậc hai sau:
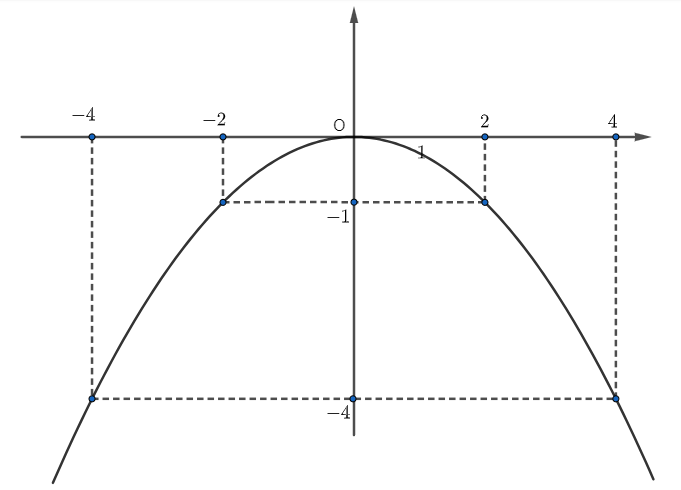
Hệ số \(a\) của đồ thị hàm số bậc hai này là
Đồ thị của hình bên dưới là đồ thị của hàm số nào trong các hàm số sau?
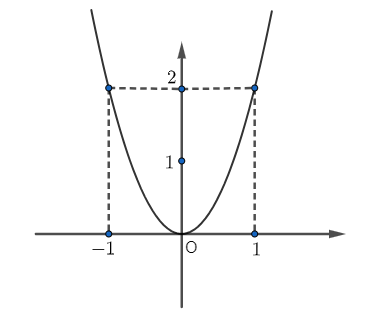
Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\,?\)
Để vẽ được đồ thị hàm số \(y = \frac{{ - 1}}{4}{x^2}\) cần xác định các điểm nào sau đây?
Cho hàm số \(y = {x^2}\) có đồ thị là \(\left( P \right).\) Đường thẳng đi qua hai điểm thuộc \(\left( P \right)\) có hoành độ bằng \( - 1\) và \(2\) là
Hàm số \(y = \left( {m + 2} \right){x^2}\) đạt giá trị nhỏ nhất khi
Trong mặt phẳng tọa độ \[Oxy\], cho hàm số \(y = \left( {m + 2} \right){x^2}\) có đồ thị đi qua điểm \(\left( { - 1\,;\,\,3} \right).\) Khi đó giá trị của \[m\] tương ứng là
Cho hàm số \(y = - 2{x^2}\) có đồ thị là \(\left( P \right).\) Tọa độ các điểm thuộc \(\left( P \right)\) có tung độ bằng \( - 6\) là