Cho hình vuông \[ABCD\] cạnh \[a.\] Khẳng định nào sau đây đúng?
A. Đường tròn đi qua cả bốn đỉnh của hình vuông \[ABCD\] cạnh \[a\] có tâm là điểm \[A\] và bán kính \[R = a\sqrt 2 .\]
B. Đường tròn đi qua cả bốn đỉnh của hình vuông \[ABCD\] cạnh \[a\] có tâm là giao điểm của hai đường chéo \[AC,\,\,BD\] và bán kính \[R = a\sqrt 2 .\]
C. Đường tròn đi qua cả bốn đỉnh của hình vuông \[ABCD\] cạnh \[a\] có tâm là điểm \[A\] và bán kính \[R = \frac{{a\sqrt 2 }}{2}.\]
D. Đường tròn đi qua cả bốn đỉnh của hình vuông \[ABCD\] cạnh \[a\] có tâm là giao điểm của hai đường chéo \[AC,\,\,BD\] và bán kính \[R = \frac{{a\sqrt 2 }}{2}.\]
Giải bởi Vietjack
Đáp án đúng là: D
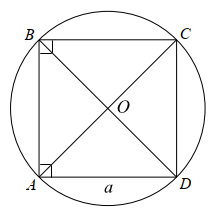
Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD\] của hình vuông \[ABCD.\]
Suy ra \[O\] là trung điểm của \[AC\] và \[BD.\]
Do đó \[OA = OC\] và \[OB = OD.\]
Mà \[AC = BD\] (do \[AC\] và \[BD\] là hai đường chéo của hình vuông \[ABCD\]).
Vì vậy \[OA = OC = OB = OD.\]
Vậy bốn điểm \[A,B,C,D\] của hình vuông \[ABCD\] cùng thuộc đường tròn tâm \[O\] bán kính \[OA.\]
Ta có \[AB = BC = a\] (do \[ABCD\] là hình vuông cạnh \[a\]).
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[B,\] ta được:
\[A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2}.\]
Suy ra \[AC = a\sqrt 2 .\] Do đó \[OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}.\]
Vậy đường tròn đi qua cả bốn đỉnh của hình vuông \[ABCD\] cạnh \[a\] có tâm là giao điểm của hai đường chéo \[AC,\,\,BD\] và bán kính \[R = \frac{{a\sqrt 2 }}{2}.\]
Do đó ta chọn phương án D.
Cho đường tròn \[\left( {O\,;R} \right)\] và một điểm \[G\] bất kì. Ta nói điểm \[G\] nằm trên đường tròn \[\left( {O\,;R} \right)\] nếu
Cho hình chữ nhật \[ABCD\] có \[AC = 16{\rm{\;cm}}.\] Biết rằng bốn điểm \[A,B,C,D\] cùng thuộc một đường tròn. Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD.\] Tâm và bán kính của đường tròn đó là
Cho tam giác \[ABC\] nhọn có các đường cao \[BD,\,\,CE.\] Khẳng định nào sau đây là đúng?
Cho đường tròn \[\left( {O;R} \right)\] và ba điểm \[A,B,C\] thuộc đường tròn đó sao cho \[\Delta ABC\] cân tại \[A.\] Giả sử \[BC = 6{\rm{\;cm}},\] đường cao \[AM\] của \[\Delta ABC\] bằng \[4{\rm{\;cm}}.\] Gọi \[B'\] là điểm đối xứng với \[B\] qua \[O.\] Kẻ \[AH \bot CB'\] tại \[H.\] Khi đó chu vi tứ giác \[AHCM\] bằng
Cho \[\Delta ABC\] cân tại \[A,\] vẽ hai đường cao \[BE\] và \[CF\] cắt nhau tại \[H.\] Gọi \[I,K\] lần lượt là hai điểm trên \[BH,CH\] sao cho \[HI = HE,HK = HF.\] Gọi \[M\] là trung điểm của \[AH.\] Khi đó \[\Delta ABC\] cần điều kiện gì để điểm \[M\] thuộc đường tròn đi qua bốn điểm \[E,F,I,K?\]
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
Cho đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và một điểm \[K\] bất kì. Biết rằng \[OK = 7{\rm{\;cm}}.\] Khẳng định nào sau đây đúng?
II. Thông hiểu
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12{\rm{\;cm}}.\) Bán kính đường tròn đi qua ba đỉnh của tam giác đó bằng
Cho đường tròn \[\left( {O;R} \right).\] Đường thẳng \[d\] đi qua tâm \[O,\] cắt đường tròn \[\left( O \right)\] tại hai điểm \[A,C.\] Đường thẳng \[d'\] (khác \[d\]) đi qua tâm \[O,\] cắt đường tròn \[\left( O \right)\] tại hai điểm \[B,D.\] Khi đó tứ giác \[ABCD\] là hình gì?
Cho đường tròn \[\left( {O;3{\rm{\;cm}}} \right)\] và điểm \[A \in \left( O \right).\] Đường thẳng \[d\] vuông góc với \[OA\] tại trung điểm của \[OA\] cắt đường tròn \[\left( O \right)\] tại \[B\] và \[C.\] Kết luận nào sau đây đúng nhất?
Cho hình vuông \[ABCD\] có \[E\] là giao điểm của hai đường chéo. Kết luận nào sau đây sai?
III. Vận dụng
Cho tam giác \[ABC\] cân tại \[A\] có \[\widehat {A\,} = 120^\circ .\] Biết rằng các đỉnh của tam giác nằm trên đường tròn tâm \[O\] bán kính \[4{\rm{\;cm}}.\] Khi đó diện tích tam giác \[ABC\] bằng
