Tọa độ hình chiếu của A(5;4) trên đường thẳng Δ: 3x + y + 1 = 0 là:
A. (1;-2)
B. (0;-1)
C. (1;-4)
D. (-1;2)
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D.
Ta có:
Δ: 3x + y + 1 = 0 ⇒ nΔ = (3;1) ⇒
Phương trình đường thẳng đi qua A(5;4) nhận 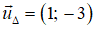
1.(x - 5) - 3.(y - 4) = 0
⇔ x - 5 - 3y + 12 = 0
⇔ x - 3y + 7 = 0
Tọa độ hình chiếu của A(5;4) trên đường thẳng Δ: 3x + y + 1 = 0 là nghiệm của hệ phương trình:
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Trong mặt phẳng Oxy, xác định điểm A' đối xứng với A(3;1) qua đường thẳng (Δ): x - 2y + 9 = 0.
Cosin của góc giữa hai đường thẳng Δ1: a1x + b1y + c1 = 0 và Δ2: a2x + b2y + c2 = 0 là:
Đường thẳng đi qua M(-2;2) và nhận vectơ làm vectơ pháp tuyến có phương trình tổng quát là:
Đường thẳng đi qua điểm D(4;1) và có hệ số góc k = -2 có phương trình tham số là:
Vectơ là vectơ pháp tuyến của đường thẳng có phương trình nào sau đây .
Đường thẳng đi qua M(2;1) và nhận vectơ làm vectơ chỉ phương có phương trình tham số là:
Đường thẳng Δ đi qua M(x0;y0) và nhận vectơ làm vectơ pháp tuyến có phương trình là:
Tìm tham số m để hai đường thẳng d: x - 2y + 4 + m = 0 và Δ: 2x - y + 3 = 0 song song với nhau.
Giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y + 5 = 0 có tọa độ là