Hàm số y = f(x) liên tục trên [2; 9]. F(x) là một nguyên hàm của hàm số f(x) trên [2; 9] và Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Sử dụng công thức với F(x) là một nguyên hàm của hàm số f(x).
Cách giải:
Vì F(x) là nguyên hàm của hàm số f(x) nên
Chọn A.
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có đạo hàm . Số điểm cực tiểu của hàm số đã cho là
Hình trụ tròn xoay có độ dài đường sinh bằng l và bán kính đáy bằng R có diện tích xung quanh cho bởi công thức
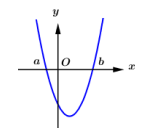
Cho hàm số bậc ba y = f(x) có đồ thị của hàm số f'(x) như hình vẽ và f(b) = 1. Số giá trị nguyên của để hàm số có đúng 5 điểm cực trị là:
Trong một hệ trục tọa độ Oxyz, cho mặt phẳng Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng