Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc 300. Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a.
A.\[d = \frac{{2a\sqrt {21} }}{{21}}.\]
B. \[d = \frac{{a\sqrt {21} }}{7}.\]
C. \[d = a.\]
D. \[d = a\sqrt 3 .\]
Giải bởi Vietjack
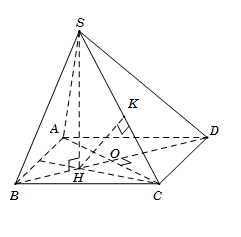
Tam giác ABC đều cạnh aa, H là trọng tâm tam giác nên \[BH = \frac{2}{3}BO = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow HD = BD - BH = a\sqrt 3 - \frac{{a\sqrt 3 }}{3} = \frac{{2a\sqrt 3 }}{3}\]
Xác định\[{30^0} = \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH}\] và\[SH = HD.\tan \widehat {SDH} = \frac{{2a\sqrt 3 }}{3}.\frac{1}{{\sqrt 3 }} = \frac{{2a}}{3}\]
Ta có:
\[\begin{array}{*{20}{l}}{BH \cap \left( {SCD} \right) = D \Rightarrow \frac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \frac{{BD}}{{HD}} = \frac{3}{2}}\\{ \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \frac{3}{2}.d\left( {H;\left( {SCD} \right)} \right)}\end{array}\]
Ta có\[HC \bot AB \Rightarrow HC \bot CD\]
Kẻ\[HK \bot SC\,\,\,\,\left( 1 \right)\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{CD \bot HC}\\{CD \bot SH}\end{array}} \right. \Rightarrow CD \bot (SHC) \Rightarrow CD \bot HK(2)\)
Từ (1) và (2)\[ \Rightarrow HK \bot \left( {SCD} \right) \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\]
Tam giác vuông SHC, có
\[HK = \frac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }} = \frac{{\frac{{2a}}{3}.\frac{{a\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\frac{{2a}}{3}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} }} = \frac{{2a\sqrt {21} }}{{21}}\]
Vậy\[d\left( {B;\left( {SCD} \right)} \right) = \frac{3}{2}HK = \frac{{a\sqrt {21} }}{7}\]
Đáp án cần chọn là: B
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) một góc \({30^0}\).Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách d từ A đến (SCD).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng \({60^ \circ }\). Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
Cho hình lập phương ABCD,A′B′C′D′ có cạnh bằng 3a. Khoảng cách từ A′ đến mặt phẳng (ABCD) bằng
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc \({60^ \circ }\)Tính khoảng cách d từ điểm D đến mặt phẳng (SBC).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \(SA = \frac{{a\sqrt {15} }}{2}\) và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC).
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng \(\frac{{a\sqrt {21} }}{6}\). Tính khoảng cách d từ đỉnh A đến mặt phẳng (SBC) .
Cho tứ diện OABC có ba cạnh OA,OB,OC đôi một vuông góc với nhau. Biết khoảng cách từ điểm O đến các đường thẳng BC,CA,AB lần lượt là \(a,a\sqrt 2 ,a\sqrt 3 \). Khoảng cách từ điểm O đến mặt phẳng (ABC) là \(\frac{{2a\sqrt m }}{{11}}\). Tìm m.
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với đáy, SA=AB=a và AD=x.a. Gọi E là trung điểm của SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) bằng \(h = \frac{a}{3}\).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh aa. Cạnh bên \(SA = a\sqrt 3 \) và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, \[AD = 2BC,\;AB = BC = a\sqrt 3 \]. Đường thẳng SA vuông góc với mặt phẳng (ABCD). Gọi E là trung điểm của cạnh SC. Tính khoảng cách d từ điểm E đến mặt phẳng (SAD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên của hình chóp bằng nhau và bằng 2a. Tính khoảng cách d từ A đến mặt phẳng (SCD)
