Cho hàm số \[y = f\left( x \right) = {\left( {{x^2} + x - 2} \right)^{\frac{2}{3}}}\]. Chọn khẳng định sai:
A.\[f'\left( 0 \right) = - \frac{2}{{3\sqrt[3]{2}}}\]
B. \[f'\left( 2 \right) = \frac{{10}}{{3\sqrt[3]{4}}}\]
C. \[f'\left( { - 3} \right) = - \frac{{10}}{{3\sqrt[3]{4}}}\]
D. \[f'\left( 3 \right) = \frac{{14}}{{3\sqrt[3]{{10}}}}\]
Giải bởi Vietjack
TXĐ: \[D = \left( { - \infty ; - 2} \right) \cup \left( {1; + \infty } \right)\]
Ta có:
\[y' = f'\left( x \right) = {\left[ {{{\left( {{x^2} + x - 2} \right)}^{\frac{2}{3}}}} \right]^\prime } = \frac{2}{3}{\left( {{x^2} + x - 2} \right)^{ - \frac{1}{3}}}{\left( {{x^2} + x - 2} \right)^\prime }\]
\[ = \frac{2}{3}{\left( {{x^2} + x - 2} \right)^{ - \frac{1}{3}}}\left( {2x + 1} \right) = \frac{{2\left( {2x + 1} \right)}}{{3\sqrt[3]{{{x^2} + x - 2}}}},\forall x \in D\]
Do đó:
\[f'\left( 2 \right) = \frac{{10}}{{3\sqrt[3]{4}}};f'\left( { - 3} \right) = - \frac{{10}}{{3\sqrt[3]{4}}};f'\left( 3 \right) = \frac{{14}}{{3\sqrt[3]{{10}}}}\] và không tồn tại \[f'\left( 0 \right)\]
Đáp án cần chọn là: A
Đẳng thức \[{\left( {\sqrt[n]{x}} \right)^\prime } = ({x^{\frac{1}{n}}})' = \frac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \frac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\] xảy ra khi:
Cho hàm số \[y = {\left( {x + 2} \right)^{ - 2}}\]. Hệ thức giữa y và y″ không phụ thuộc vào x là:
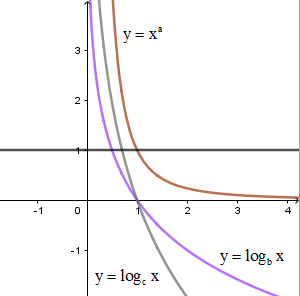
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
Cho hàm số \[f\left( x \right) = {\left( {{x^{1 + \frac{1}{{2{{\log }_4}x}}}} + {8^{\frac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\frac{1}{2}}} - 1\] với \[0 < x \ne 1\]. Tính giá trị biểu thức \[P = f\left( {f\left( {2018} \right)} \right).\]
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
Cho hàm số \[y = {x^{e - 3}}\]. Trong các kết luận sau kết luận nào sai?
Tìm TXĐ của hàm số \[y = {\left( {{x^3} - 27} \right)^{\frac{\pi }{2}}}\]
Xét hàm số \[y = {x^\alpha }\] trên tập \[\left( {0; + \infty } \right)\;\]có đồ thị dưới đây, chọn kết luận đúng:
