Cho (O;R), AB là dây cung của đường (O) sao cho AB = . M là một điểm trên cung lớn AB. Số đo cung là bao nhiêu?
A. 30°
B. 60°
C. 45°
D. 240°
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
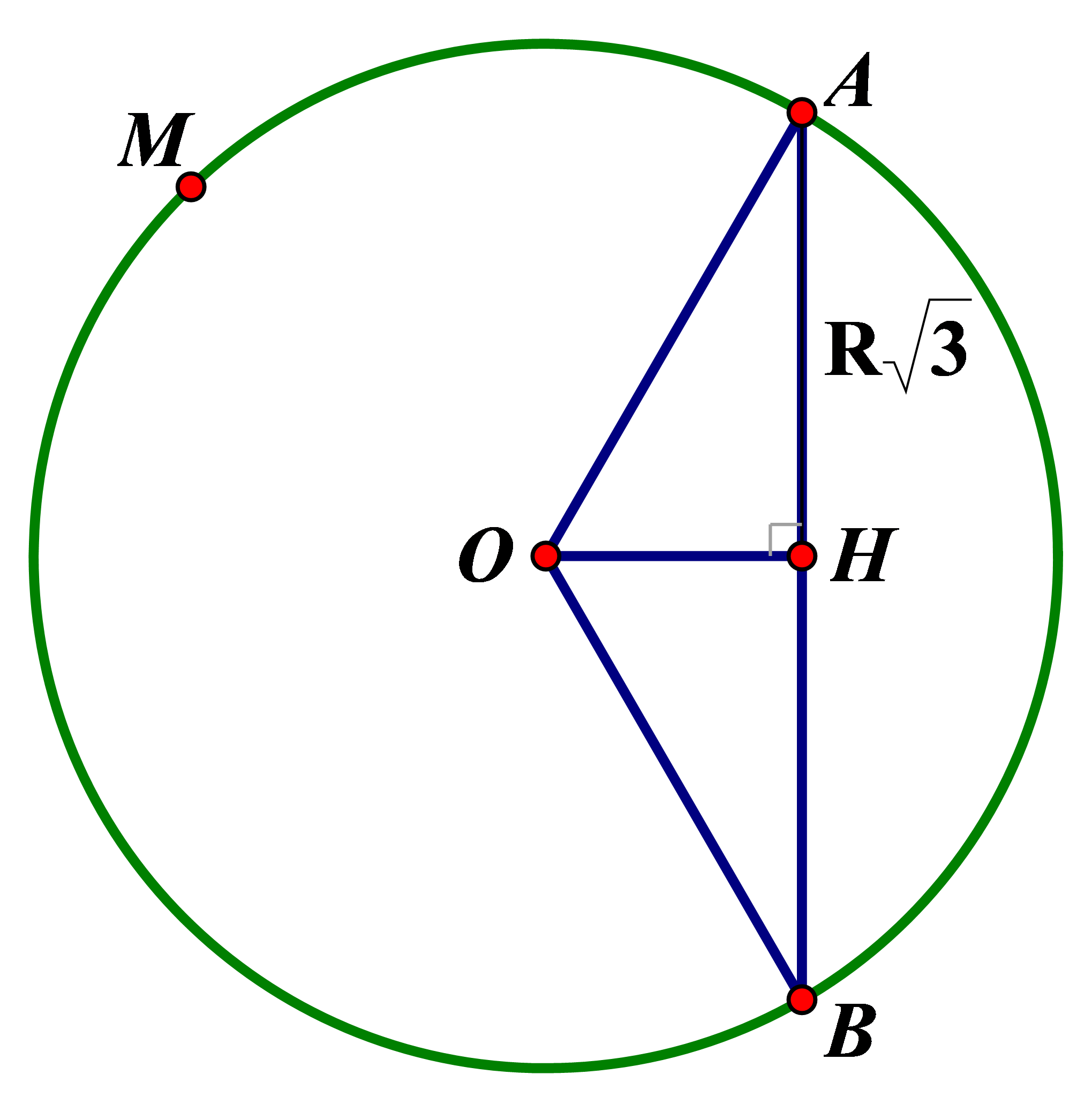
Kẻ OH vuông góc AB ().
Ta có:
H là trung điểm AB (đường kính vuông góc dây cung thì đi qua trung điểm của dây)
Suy ra AH = .
sin = ⇒ = 60°.
Ta có: OA = OB = R.
Suy ra tam giác OAB cân.
Tam giác OAB có OH là đường cao suy ra OH cũng là đường phân giác
Do đó 2. 60° = 120°.
Số đo cung nhỏ == 120°.
Số đo cung = 360° − Số đo cung nhỏ = 360 – 120 = 240°.
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là tiếp điểm) và cát tuyến AMN không qua O (M nằm giữa A và N). Gọi H là giao điểm của OA và BC. Chứng minh rằng.
a. Tứ giác ABOC nội tiếp.
b. OA ⊥ BC
c. AB2 = AM.AN
d.
Điểm A thuộc nửa đường tròn (O;6cm) đường kính BC sao cho diện tích ΔABC lớn nhất. Khi đó số đo cung là:
Hai tủ sách có 450 quyển sách, nếu chuyển 50 quyển từ tủ một sang tủ hai thì hai tủ có số sách bằng nhau. Số sách của tủ một là:
Các cặp số (x; y) sau, cặp nào là nghiệm của phương trình x + 2y = 3?
Hai khách du lịch xuất phát đồng thời từ hai thành phố A và B cách nhau 53km. Họ đi ngược chiều và gặp nhau sau 2h. Hỏi vận tốc của mỗi người, biết rằng khi gặp nhau người thứ hai đi được nhiều hơn người thứ nhất 3km.
Số giá trị nguyên cùa m để đồ thị hàm số y = (2 – m2)x2 nằm phía trên trục hoành là:
Cho (P): y = x2 và (d): y = x – 4
a. Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Giải các phương trình, hệ phương trình sau:
a.
b. 2x2 – 9x – 5 = 0