Cho đường tròn (O; R), đường kính BC cố định và điểm A cố định thuộc đoạn thẳng OB (A không trùng với O và B). Kẻ dây PQ ⊥ BC tại A. Lấy M thuộc cung lớn PQ (M không trùng với C). Nối BM cắt PQ tại E. Chứng minh:

a. Tứ giác AEMC nội tiếp

b. BP² = BE. BM = BA.BC

c. Từ E kẻ đường thẳng song song BC cắt PC tại I. Chứng minh: và tâm đường tròn ngoại tiếp tam giác EPM nằm trên một đường thẳng cố định khi M di chuyển trên cung lớn PQ.

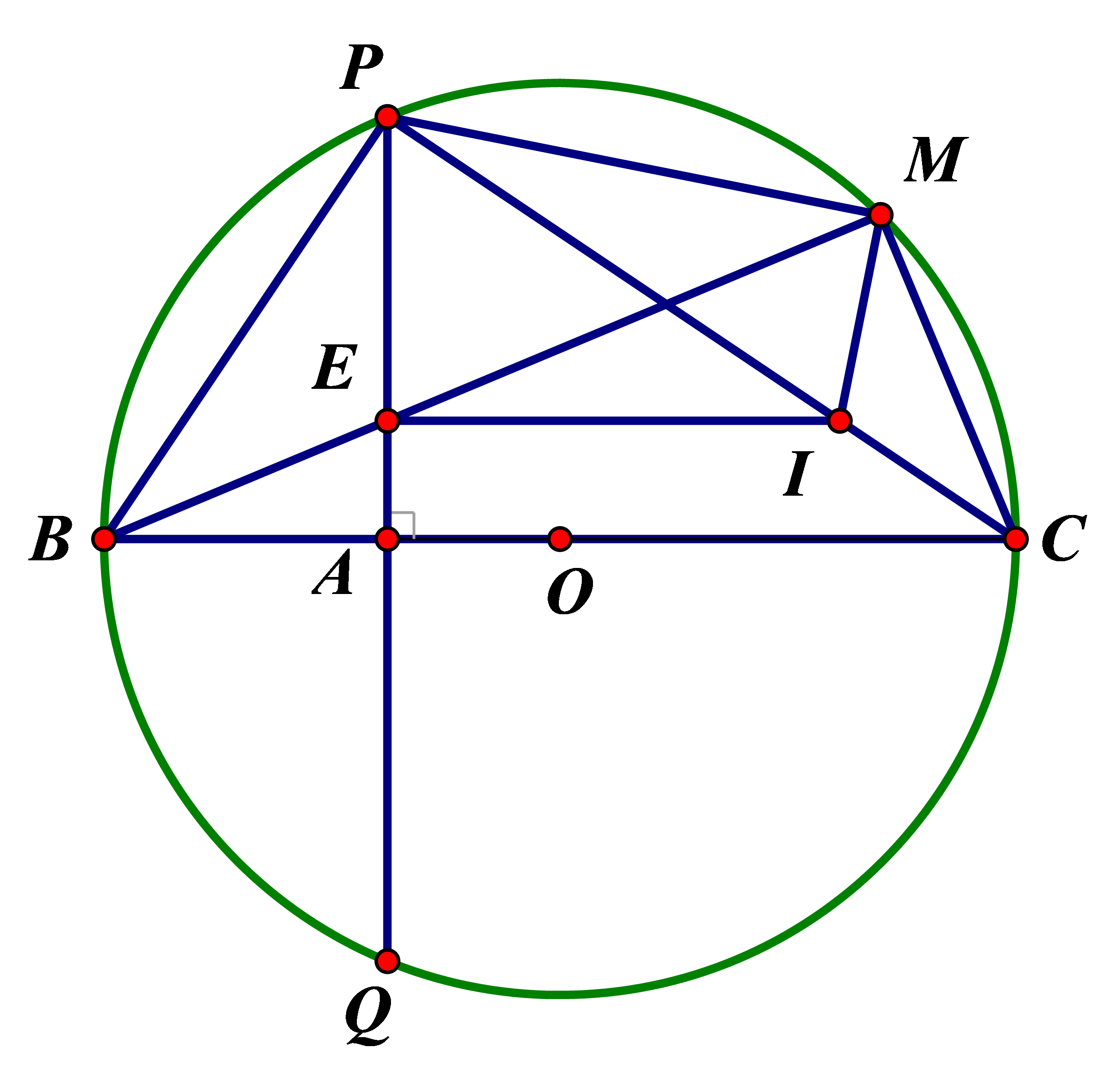
a. $\widehat{\text{EAC}}$ = 90° (EA vuông góc AC)

$\widehat{EMC}$= 90° (Góc nội tiếp chắn nửa đường tròn)

Xét tứ giác ABOC có $\widehat{\text{EAC}}$ + $\widehat{\text{EMC}}$ = 90° + 90° = 180°

Suy ra tứ giác AEMC nội tiếp (đpcm).

b. Xét ∆ BAP và ∆ BPC có:

$\widehat{\text{PBC}}$là góc chung

$\widehat{BPC}=\widehat{BAC}$= 90° (  là góc nội tiếp chắn nửa đường tròn)

Suy ra ∆ BAP  ∆ BPC (g.g)

Từ đó suy ra $\frac{BA}{BP}=\frac{BP}{BC}\iff B{P}^2=BA.BC$ (1)

Xét ∆ BEA và ∆ BCM có:

$\widehat{\text{MBC}}$ là góc chung

 $\widehat{BEA}=\widehat{BCM}$(tứ giác AEMC nội tiếp)

Suy ra ∆ BEA đồng dạng ∆ BCM (g.g)

Từ đó suy ra $\frac{BE}{BC}=\frac{BA}{BM}\iff BE.BM=BA.BC$ (2)

Từ (1) và (2) suy ra: BP² = BE. BM = BA.BC (đpcm)

c. Ta có:

$\widehat{EMI}=\widehat{MBC}$(hai góc đồng vị).

$\widehat{MPC}=\widehat{MBC}$(tứ giác PMCB nội tiếp đường tròn O).

Suy ra $\widehat{MEI}=\widehat{MPC}$  .

Tứ giác EPMI có $\widehat{MEI}=\widehat{MPI}$ suy ra tứ giác EPMI nội tiếp.

Ta có: $\begin{array}{l}PA\perp BC\\ BC//EI\end{array}\}\Rightarrow PA\perp EI\Rightarrow \widehat{PEI}$ = 90°

Ta có tâm đường tròn ngoại tiếp tam giác EPM cũng là tâm của đường tròn ngoại tiếp tứ giác EPMI.

Mà ta có $\widehat{PEI}$ = 90° dẫn đến PI là đường kính .

Suy ra tâm của đường tròn ngoại tiếp tam giác EPM là trung điểm của PI.

Mà điểm này cũng thuộc đường thẳng PC với P và C cố định nên ta suy ra điều phải chứng minh.