Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
A.\[ - x - 3y = 0\]
B. \[3x + y + 3z - 6 = 0\]
C. \[15x - y - 3z - 12 = 0\]
D. \[15x - y - 3z - 12 = 0\]
Giải bởi Vietjack
Phương trình mặt phẳng (ABC) qua B(1,0,1) và nhận\[\vec n = [\overrightarrow {AB} ,\overrightarrow {AC} ]\] là vectơ pháp tuyến.
Ta có\[\overrightarrow {AB} = (0,3, - 1)\]và\[\overrightarrow {AC} = (1,6, - 2)\]. Suy ra\[\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0, - 1, - 3} \right)\]
Quan sát đáp án bài cho, ta chọn ngay đáp án D.
Đáp án cần chọn là: D
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với \[\left( Q \right):x + 2y - 3z + 1 = 0\;\]và \[\left( R \right):2x - 3y + z + 1 = 0\;\].
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2), B(2,−3,−2). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng \[(P):2x - y + 3z + 4 = 0\] là:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x′Ox,y′Oy,z′Oz lần lượt tại các điểm A,B,C sao cho \[OA = OB = OC \ne 0\]?
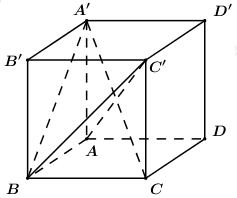
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận \[\overrightarrow n = \left( { - 2,4,1} \right)\;\]làm vectơ pháp tuyến.
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1) . Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x - y + 3 = 0\]. Vec-tơ nào sau đây không là vecto pháp tuyến của mặt phẳng (P) .
Cho mặt phẳng \[\left( \alpha \right)\;\]đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng \[\left( \alpha \right)\;\]tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng \[\left( \alpha \right)\]
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
Trong hệ trục toạ độ không gian Oxyz, cho \[A\left( {1,0,0} \right),B\left( {0,b,0} \right),C\left( {0,0,c} \right),\] biết b,c>0, phương trình mặt phẳng \[\left( P \right):y - z + 1 = 0\;\]. Tính \[M = c + b\] biết \[\left( {ABC} \right) \bot \left( P \right),\;d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{3}\]
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng \[(Q):19x - 6y - 4z + 27 = 0\;\]và \[(R):42x - 8y + 3z + 11 = 0\;\]là:
Trong không gian Oxyz, hai mặt phẳng \[4x - 4y + 2z - 7 = 0\;\]và \[2x - 2y + z + 4 = 0\;\]chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
Trong không gian Oxyz, cho ba mặt phẳng \[\left( P \right):x + y + z - 1 = 0,\;\left( Q \right):2x + my + 2z + 3 = 0\;\]và \[\left( R \right): - x + 2y + nz = 0\]. Tính tổng \[m + 2n\], biết \[\left( P \right) \bot \left( R \right)\;\]và \[\left( P \right)//\left( Q \right)\]
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho\[M{A^2} - M{B^2} = 2\]. Tìm khẳng định đúng.
