A. Hàm số đồng biến trên (1; + ∞) ;
B. Đồ thị hàm số có trục đối xứng x = – 2;
C. Hàm số nghịch biến trên (– ∞; 1);
D. Đồ thị hàm số có đỉnh I(1; – 2).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có a = 1 > 0; b = – 2; c = – 1.
Vì a = 1 > 0 nên
Hàm số đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) hay (1; + ∞). Đáp án A đúng
Hàm số nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) hay (– ∞; 1). Đáp án C đúng
Tọa độ đỉnh xI = \( - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\) và yI = \( - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{( - 2)}^2} - 4.1.( - 1)}}{{4.1}} = - 2\).
Vậy toạ độ đỉnh I(1; - 2)
Đáp án D đúng
Đồ thị hàm số có trục đối xứng là \[x = - \frac{b}{{2a}} = 1\]. Đáp án B sai
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
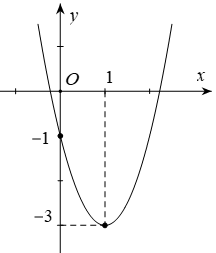
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).