Trong một đường tròn cho trước, hãy nội tiếp một hình chữ nhật có diện tích lớn nhất.
Giải bởi Vietjack
Gọi bán kính đường tròn là R và cạnh AB của hình chữ nhật cần tìm là x. Theo định lí Pythagore, ta có: , từ đó suy ra biểu thức của diện tích S là .
Hàm số này và hàm số đạt giá trị cực đại với cùng một giá trị của x. Mà .
Đặt , ta có: .
Nghĩa là đạt được khi tức là khi .
Ta nhận thấy rằng khi thì , ta nhìn thấy hình chữ nhật cần tìm là hình vuông. Hay ta có kết luận: “Trong các hình chữ nhật nội tiếp cùng một đường tròn thì hình vuông có diện tích lớn nhất”.
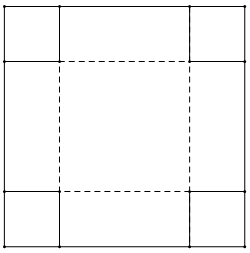
Từ một miếng bìa hình vuông cạnh a, người ta cắt bốn góc những hình vuông bằng nhau sao cho phần còn lại của miếng bìa theo những đường chấm thành một hộp có thể tích lớn nhất (hình vẽ).
Ba con đường cắt nhau tạo ra một tam giác. Trong tam giác đó phải đặt xí nghiệp ở đâu để tổng độ dài các con đường từ xí nghiệp ra các con đường là ngắn nhất?
Người ta đào một con mương với thiết diện cắt ngang là một hình thang cân, đáy và cạnh bên có cùng độ dài là a. Độ dài của đáy lớn (bề ngang của mặt mương) hình thang là bao nhiêu để diện tích của mặt cắt là lớn nhất (cho lưu lượng nước thoát qua lớn nhất).
Hãy chọn hướng mở một con đường đi qua thành phố sao cho tổng các khoảng cách từ nó tới hai điểm dân cư đã có là nhỏ nhất.
Bên cạnh một con sông đào thẳng người ta phải làm một khu vườn hình chữ nhật có diện tích cho trước S. Người ta muốn rào khu vườn bằng hàng rào ngắn nhất là bao nhiêu? Biết rằng về phía sông thì không phải làm hàng rào.
Từ tất cả hình chữ nhật với chu vi đã cho, thì hình vuông có diện tích lớn nhất.
