Giải bởi Vietjack
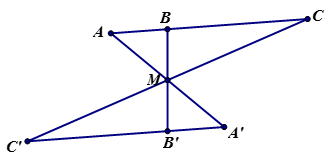
Giả sử A, B, C thẳng hàng theo thứ tự đó, ta có AB + BC = AC (1).
Các đoạn thẳng A’B’, B’C’ và A’C’ lần lượt đối xứng với các đoạn thẳng AB, BC, AC qua điểm M nên ta có A’B’ = AB, B’C’ = BC, A’C’ = AC.
Kết hợp đẳng thức (1) ta được A’B’ + B’C’ = A’C’. Vậy A’, B’, C’ thẳng hàng.
Cho tam giác ABC vuông tại A ( AB < AC), điểm D thuộc cạnh huyền BC. Vẽ điểm M và điểm N đối xứng với D lần lượt qua AB và AC. Chứng minh rằng:
a) M và N đối xứng qua A.
Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng: E là điểm đối xứng của F qua C.
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.
a) Chứng minh AE = AF;
