Giải bởi Vietjack
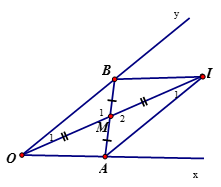
Cách dựng:
- Dựng điểm I đối xứng với O qua điểm M.
- Qua I dựng đường thẳng song song với Oy cắt Ox ở A.
- Dựng đường thẳng AM cắt Oy ở B.
Chứng minh:
Xét và có:
( hai góc so le trong)
MO = MI ( Vì I và O đối xứng nhau qua M)
( hai góc đối đỉnh)
=> (g.c.g) => MA = MB ( 2 cạnh tương ứng)
Bài toán luôn luôn dựng được một và có một nghiệm hình.
Cho tam giác ABC vuông tại A ( AB < AC), điểm D thuộc cạnh huyền BC. Vẽ điểm M và điểm N đối xứng với D lần lượt qua AB và AC. Chứng minh rằng:
a) M và N đối xứng qua A.
Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng: E là điểm đối xứng của F qua C.
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.
a) Chứng minh AE = AF;
