7 câu hỏi trắc nghiệm thuộc Dạng 4: Bài nâng cao phát triển tư duy có đáp án

Bài tập Toán 8 Chủ đề 9: Đối xứng tâm có đáp án

Dạng 4: Bài nâng cao phát triển tư duy có đáp án

752 lượt thi
7 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Cho ba điểm A, B, C thẳng hàng và điểm M không thuộc đường thẳng đó. Gọi A’, B’, C’ lần lượt là điểm đối xứng của A, B, C qua M. Chứng minh A’, B’, C’ thẳng hàng.

Xem đáp án

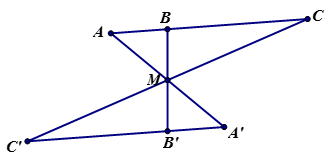
Cho ba điểm A, B, C thẳng hàng và điểm M không thuộc đường thẳng đó. Gọi A’, B’, C’ lần lượt là điểm đối xứng của A, B, C qua M. (ảnh 1)

Giả sử A, B, C thẳng hàng theo thứ tự đó, ta có AB + BC = AC (1).

Các đoạn thẳng A’B’, B’C’ và A’C’ lần lượt đối xứng với các đoạn thẳng AB, BC, AC qua điểm M nên ta có A’B’ = AB, B’C’ = BC, A’C’ = AC.

Kết hợp đẳng thức (1) ta được A’B’ + B’C’ = A’C’. Vậy A’, B’, C’ thẳng hàng.

Câu 2:

Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK. Chứng minh rằng điểm I đối xứng với điểm K qua AH.

Xem đáp án

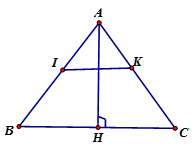
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK. (ảnh 1)

Vì ABC cân tại A, AH là đường cao nên AH là tia phân giác của góc A

Lại có: IA = AK => $△$ IAK cân tại A, mà AH là tia phân giác của góc A (cmt) => AH là đường trung trực của IK => Điểm I đối xứng với điểm K qua AH

Câu 3:

Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng: E là điểm đối xứng của F qua C.

Xem đáp án

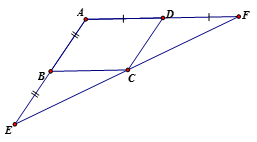
Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. (ảnh 1)

E là điểm đối xứng của A qua B (gt) nên AB = BE

Tứ giác ABCD là HBH => $\{\begin{cases} A B ∥ C D \\ A B = C D \end{cases}$

Mà AB = BE (cmt) $\Rightarrow \{\begin{cases} B E ∥ C D \\ B E = C D \end{cases}$ => Tứ giác BDCE là hình bình hành

=> BD // EC và BD = EC.

Chứng minh tương tự cũng có BD // CF và BD = CF.

Vì BD // EC và BD // CF => E, C, F thẳng hàng (tiên đề Ơ-clit) Mà EC = CF (= BD) nên C là trung điểm EF => E là điểm đối xứng của F qua C.

Câu 4:

Cho hình bình hành ABCD. Gọi E, F lần lượt trên các cạnh AD, BC sao cho AE = CF. Chứng minh rằng: các đường thẳng AC, BD, EF đồng quy.

Xem đáp án

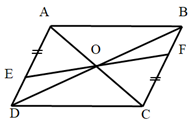
Cho hình bình hành ABCD. Gọi E, F lần lượt trên các cạnh AD, BC sao cho AE = CF. (ảnh 1)

Gọi O là giao điểm cuả AC, BD.

Tứ giác ABCD là hình bình hành(gt) => O là trung điểm của AC

Tứ giác AECF có AE = CF, AE // CF nên là hình bình hành (dhnb)

mà O là trung điểm AC nên O là trung điểm EF.

=> EF đi qua O. Vậy các đường thẳng AC, BD, EF đồng quy tại điểm O.

Câu 5:

Cho góc xOy khác góc bẹt và điểm M nằm trong góc đó. Hãy dựng qua M một đường thẳng cắt Ox ở A, cắt Oy ở B sao cho M là trung điểm của AB.

Xem đáp án

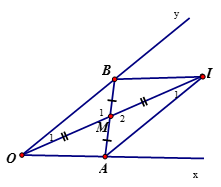
Cho góc xOy khác góc bẹt và điểm M nằm trong góc đó. Hãy dựng qua M một đường thẳng cắt Ox ở A, (ảnh 1)

Cách dựng:

- Dựng điểm I đối xứng với O qua điểm M.

- Qua I dựng đường thẳng song song với Oy cắt Ox ở A.

- Dựng đường thẳng AM cắt Oy ở B.

Chứng minh:

Xét $Δ M A I$ và $Δ M B O$ có:

$\hat{O_{1}} = \hat{I_{1}}$ ( hai góc so le trong)

MO = MI ( Vì I và O đối xứng nhau qua M)

$\hat{M_{1}} = \hat{M_{2}}$ ( hai góc đối đỉnh)

=> $Δ M A I = Δ M B O$ (g.c.g) => MA = MB ( 2 cạnh tương ứng)

Bài toán luôn luôn dựng được một và có một nghiệm hình.

Câu 6:

Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.

a) Chứng minh AE = AF;

Xem đáp án

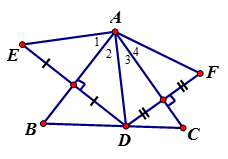
Cho tam giác ABC, D là một điểm trên cạnh BC. a) Chứng minh AE = AF; (ảnh 1)

a) E đối xứng với D qua AB => AB là trung trực của ED => AE = AD.

F đối xứng với D qua AC => AC là trung trực của DE => AF = AD.

=> AE = AF.

Xét $Δ A E D$ cân tại A, có AB là trung trực => AB đồng thời là phân giác của $\hat{E A D}$

=> $\hat{A_{1}} = \hat{A_{2}}$

Xét $Δ A D F$ cân tại A, có AC là trung trực => AC đồng thời là phân giác của $\hat{F A D}$

=> $\hat{A_{3}} = \hat{A_{4}}$

=> $\hat{E A F} = \hat{A_{1}} + \hat{A_{2}} + \hat{A_{3}} + \hat{A_{4}} = 2 (\hat{A_{2}} + \hat{A_{3}}) = 2 \hat{B A C}$

Câu 7:

Cho tam giác ABC vuông tại A ( AB < AC), điểm D thuộc cạnh huyền BC. Vẽ điểm M và điểm N đối xứng với D lần lượt qua AB và AC. Chứng minh rằng:

a) M và N đối xứng qua A.

Xem đáp án

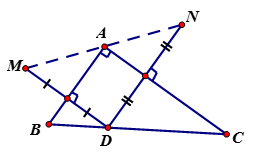
a) AM đối xứng với AD qua AB nên $\{\begin{cases} A M = A D \\ \hat{A_{1}} = \hat{A_{2}} \end{cases}$ (1)

AN đối đối xứng với AD qua AC nên $\{\begin{cases} A N = A D \\ \hat{A_{3}} = \hat{A_{4}} \end{cases}$ (2)

Từ (1) và (2) $\Rightarrow A M = A N$ và $\hat{M A N} = 2 (\hat{A_{2}} + \hat{A_{3}}) = 2 \hat{B A C} = {2.90}^{0} = 180^{0}$

=> 3 điểm M, A, N thẳng hàng

=> Mà AM = AN => M và N đối xứng qua A và MN = 2 AD.

Bắt đầu thi ngay