8 câu hỏi trắc nghiệm thuộc Dạng 5: Bài tập tự luyện có đáp án

Câu 1:

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt hai cạnh đối AD, BC ở E, F. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm O.

Xem đáp án

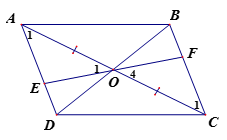
Ta có ABCD là hình bình hành

=> AD//BC

=> $\hat{A_{1}} = \hat{C_{1}}$ (2 góc so le trong)

O là giao điểm của 2 đường chéo

=> OA = OC

Xét $△$ AOE và $△$ COF có

$\hat{A_{1}} = \hat{C_{1}}$ (cmt)

OA = OC (cmt)

OA = OC (2 góc đối đỉnh)

=> $△$ AOE = $△$ COF (g.c.g)

=> OE = OF

Do đó E đối xứng với F qua O

Câu 2:

Cho tam giác ABC, D là một điểm trên BC, Qua D vẽ DE //AB (E thuộc AC) vẽ DF//AC (F thuộc AB). Gọi I là trung điểm của AD. Chứng minh rằng E đối xứng với F qua điểm I.

Xem đáp án

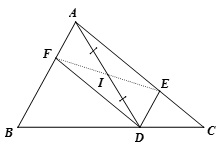
Cho tam giác ABC, D là một điểm trên BC, Qua D vẽ DE //AB (E thuộc AC) vẽ DF//AC (F thuộc AB). (ảnh 1)

Xét tứ giác AEDF có

AF//DE (DE//AB)

AE//DF (DF//AC)

=> Tứ giác AEDF là hình bình hành

Có I là trung điểm của đường chéo AD

=> I là trung điểm của đường chéo EF

Do đó E đối xứng với F qua điểm I.

Câu 3:

Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là điểm bất kỳ nằm trong tam giác ABC. Vẽ M đối xứng với O qua D, vẽ N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Xem đáp án

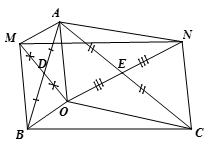
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là điểm bất kỳ nằm trong tam giác ABC (ảnh 1)

Xét tứ giác AOCN có

AE = EC (gt)

OE = EN (N đối xứng với O qua E)

=> Tứ giác AOCN là hình bình hành

AO // NC; AO = NC (1)

Xét tứ giác AOBM có

AD = DB (gt)

OD = DM (N đối xứng với O qua E)

=> Tứ giác AOBM là hình bình hành

=> AO // MB; AO = MB (1)

Từ (1) và (2) => BM // CN; BM = CN

Xét tứ giác MNCB có

BM // CN (cmt)

BM = CN (cmt)

Do đó tứ giác MNCB là hình bình hành

Câu 4:

Cho tam giác ABC có đường cao BD và CE cắt nhau tại H. Qua B vẽ đường thẳng vuông góc với AB, Qua C vẽ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau tại G. Gọi I là trung điểm của BC. Chứng minh rằng G đối xứng với H qua I.

Xem đáp án

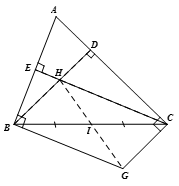
Ta có $B D ⊥ A C$ (gt)

$C G ⊥ A C$ (gt)

=> BD//CG => BH//CG

Ta có $C E ⊥ A B$ (gt)

$B G ⊥ A B$ (gt)

=> CE//BG => CH//BG

Xét tứ giác BHCG có

BH // CG (cmt)

CH // BG (cmt)

=> Tứ giác BHCG là hình bình hành

Có I là trung điểm của đường chéo BC

=> I là trung điểm GH

=> G đối xứng với H qua điểm I

Câu 5:

Cho $\hat{x O y}$ , điểm A nằm trong góc đó, Vẽ điểm B đối xứng với A qua Ox, C đối xứng với A qua Oy.

a) Chứng minh rằng OB = OC

Xem đáp án

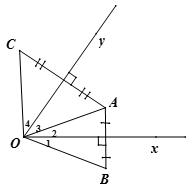
Cho xOy, điểm A nằm trong góc đó, Vẽ điểm B đối xứng với A qua Ox, C đối xứng với A qua Oy. a) Chứng minh rằng OB = OC (ảnh 1)

a) Ta có B đối xứng với A qua Ox

=> Ox là đường trung trực của AB

=> OA = OB (1)

Ta có C đối xứng với A qua Oy

=> Oy là đường trung trực của AC

=> OA = OC (2)

Từ (1) và (2) suy ra OB = OC

Câu 6:

b) Tính số đo

\hat{x O y}

để B đối xứng với C qua O

Xem đáp án

b) Xét $△$ AOB có

OA = OB (cmt)

=> $△$ AOB cân tại O

Ta lại có Ox là trung trực của AB

=> Ox là tia phân giác của $\hat{A O B}$

=> $\hat{O_{1}} = \hat{O_{2}}$ (3)

Xét $△$ AOC Có

OA = OC (cmt)

=> $△$ AOB cân tại O

Ta lại có Oy là trung trực của AC

=> Oy là tia phân giác của $\hat{A O C}$

=> $\hat{O_{3}} = \hat{O_{4}}$ (4)

Ta có $\hat{B O C} = \hat{O_{1}} + \hat{O_{2}} + \hat{O_{3}} + \hat{O_{4}} (5)$

Từ (3)(4) và (5) suy ra

$\begin{array}{l} \hat{B O C} = \hat{O_{2}} + \hat{O_{2}} + \hat{O_{3}} + \hat{O_{3}} \\ = 2 (\hat{O_{2}} + \hat{O_{3}}) \\ = 2. \hat{x O y} \end{array}$

Ta có OB = OC (cmt)

Để B đối xứng với C qua điểm O

$\Rightarrow \hat{B O C} = 180^{0}$

$\begin{array}{l} 2. \hat{x O y} = 180^{0} \\ \hat{x O y} = 180^{0} : 2 \\ \hat{x O y} = 90^{0} \end{array}$

Vậy $\hat{x O y} = 90^{0}$ thì B đối xứng với C qua O

Câu 7:

Cho $△$ ABC có H là trực tâm. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo $\hat{A B K}$ ; $\hat{A C K}$

Xem đáp án

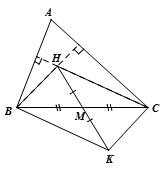
Cho ABC có H là trực tâm. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo ABK, ACK (ảnh 1)

Xét tứ giác BHCK có

MB = MC (gt)

HM = MK ( H đối xứng mới K qua M)

=> Tứ giác BHCK là hình bình hành

=> BH // CK; CH // BK (1)

Ta có H là trực tâm của ABC

=> $B H ⊥ A C; C K ⊥ A B$ (2)

Từ (1) và (2) suy ra $C K ⊥ A C; B K ⊥ A B$

=> $\hat{A B K} = 90^{0}; \hat{A C K} = 90^{0}$

Câu 8:

Cho hình thang ABCD (AD//BC). Gọi M, N lần lượt là trung điểm của các cạnh AB, CD; E là một điểm bất kỳ trên cạnh đáy AD và I, K là điểm đối xứng với E lần lượt qua M và N. Chứng minh rằng độ dài IK không phụ thuộc vào vị trí của điểm E

Xem đáp án

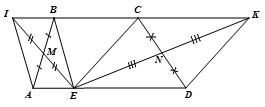
Cho hình thang ABCD (AD//BC). Gọi M, N lần lượt là trung điểm của các cạnh AB, CD; E là một điểm bất kỳ trên cạnh đáy AD và I, K (ảnh 1)

Xét tứ giác AIBE có

IM = ME (I đối xứng với E qua M )

MA = MB (gt)

=> Tứ giác AIBE là hình bình hành

=> IB = AE; AE // IB (1)

Xét tứ giác ECKD có

EN = NK ( E đối xứng với K qua N)

CN = ND (gt)

=> Tứ giắc ECKD là hình bình hành

=> CK = ED; CK // ED (2)

Ta có

IB // AE (cmt) => IB // AD

BC // AD (gt)

Theo tiên đề Oclit => I, B, C thẳng hàng

CK // ED (cmt) => CK // AD

CB // AD (gt)

Theo tiên đề Oclit => K, C, B thẳng hàng

=> I, K, C, B thẳng hàng

=> IK = IB+ CB+ CK (3)

Từ (1) (2) và (3)

=> IK = EA + CB + EB

=> IK = AD + CB

Vậy độ dài IK không phụ thuộc vào vị trí của điểm E.