Giải bởi Vietjack
Đáp án A
Phương pháp:
\[d||a \subset \left( P \right) \Rightarrow d||\left( P \right).\]
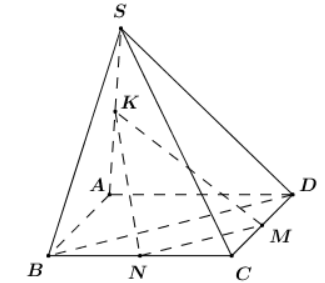
Cách giải:
MN là đường trung bình của \[\Delta BCD \Rightarrow MN||BD.\]
Mà \[MN \subset \left( {MNK} \right) \Rightarrow BD||\left( {MNK} \right).\]
Cho hình chóp S.ABCD có đáy ABCD là hình thang, biết AB song song với CD và \[AB = 2CD,\] O là giao điểm của AC và BD. Gọi M, N là trung điểm của SB và SD.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right).\]
b) Xác định giao điểm của SC và \[\left( {AMN} \right).\]
c) Gọi G là trọng tâm \[\Delta SBC.\] Chứng minh rằng OG song song với mặt phẳng \[\left( {SCD} \right).\]
Giải các phương trình sau:
a) \[\cos x = \frac{{\sqrt 3 }}{2}\] b) \[\cos 2x + \sin x + 2 = 0\]
