Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên SB, SC. Đường kính MN thay đổi của mặt cầu (T) ngoại tiếp khối đa diện ABCB1C1 và I là điểm cách tâm mặt cầu (T) một khoảng bằng ba lần bán kính. Tính giá trị nhỏ nhất của IM + IN.
A.
B.
C. 6
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
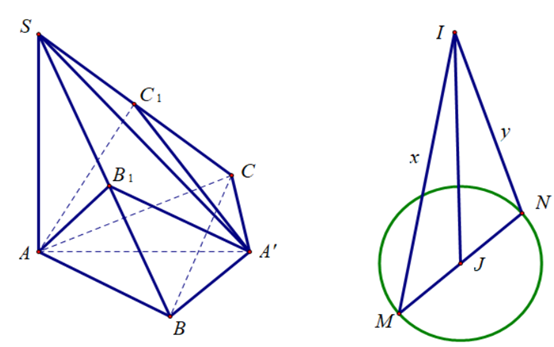
Ta có .
Bán kính đường tròn ngoại tiếp tam giác ABC: .
Gọi J là tâm đường tròn ngoại tiếp tam giác ABC, A' là điểm đối xứng của A qua J.
Ta dễ dàng chứng minh được: đều thuộc mặt cầu tâm J, đường kính .
Đặt .
+ Nếu I, J, M, N thẳng hàng thì .
+ Nếu I, J, M, N không thẳng hàng thì
.
Vậy, ta luôn có: .
Do .
.
Vậy .
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới.
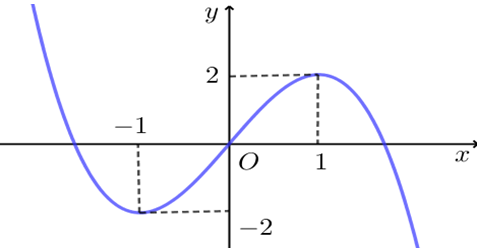
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình nghiệm đúng với ?
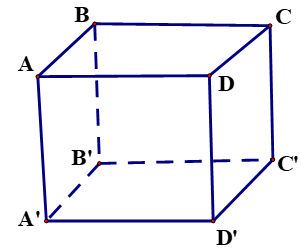
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BDD'B') bằng
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới.
![Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thực phân biệt của phương trình f[f(x) + 1] + 2 = 0 là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid2-1683044394.png)
Số nghiệm thực phân biệt của phương trình là
Cho hàm số y = f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:

Khi đó hàm số y = f(x) đồng biến trên khoảng