Giải bởi Vietjack
Lời giải
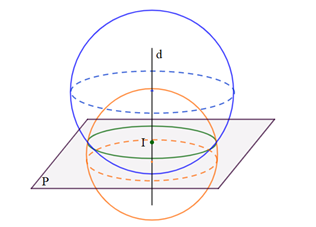
Có vô số mặt cầu chứa một đường tròn cho trước. Tâm các mặt cầu ấy nằm trên trục của đường tròn (đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn).
Cho các khẳng định:
(I): Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
(II): Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
(III): Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng thì chúng thẳng hàng.
Số khẳng định sai trong các khẳng định trên là:
Tìm công thức hàm số bậc hai, biết:
a) Đồ thị hàm số đi qua 3 điểm A(1; −3), B(0; −2), C(2; −10).
b) Đồ thị hàm số có trục đối xứng là đường thẳng x = 3, cắt trục tung tại điểm có tung độ bằng −16 và một trong hai giao điểm với trục hoành có hoành độ là −2.
Cho x, y không âm thỏa mãn: x2 + y2 = 2. Tìm GTNN, GTLN của
\(A = \frac{{{x^2} + {y^2} + 1}}{{xy + 1}}\).
Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh DABD = DACD.
b) Chứng minh rằng AM = 2.BD.
c) Tính số đo \[\widehat {MAD}\].
