Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên $ℝ$  và thoả mãn $\underset{0}{\overset{4}{\int }}f\left(x\right)\text{d}x=F\left(4\right)-G\left(0\right)+2m$ , với m > 0. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y=F\left(x\right)$ , $y=G\left(x\right)$ ; $x=0$  và $x=4$ . Khi S = 8 thì m bằng

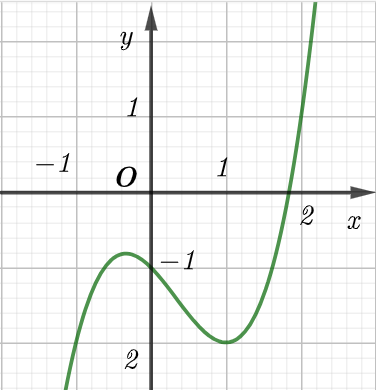
Cho hàm số $y=a{x}^3+b{x}^2+cx+d$  có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là

Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn $\left|z+2-3i\right|=4$ là một đường tròn. Tâm của đường tròn đó có tọa độ là

Cho hàm số y = f(x) liên tục trên $ℝ$ , thỏa mãn $f^{\text{'}}\left(x\right)-f\left(x\right)=-8+16x-4x^2$  và $f\left(0\right)=0$ . Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục Ox quay quanh Ox bằng

Khối lập phương có độ dài đường chéo là $3\sqrt{3}$ . Thể tích của khối lập phương đã cho là

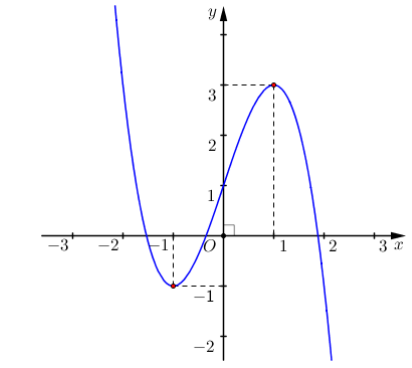
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên dương của m để phương trình f(x) = m có ba nghiệm phân biệt?

Một nhóm gồm 2 người đàn ông, 3 người phụ nữ và 4 trẻ em. Chọn ngẫu nhiên 4 người từ nhóm đó. Xác suất để 4 người được chọn: có cả đàn ông, phụ nữ và trẻ em bằng

Trong không gian Oxyz, cho A(1;2;3). Điểm đối xứng với A qua trục Oz có tọa độ là

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=x^4-4x^3+\left(4-m\right)x+1$  có ba điểm cực trị?

Trên tập hợp số phức, xét phương trình $z^2-2\left(m+1\right)z+m^2+2=0$  (m tham số). Có tất cả bao nhiêu giá trị của tham số m để phương trình có hai nghiệm phân biệt $z_1;z_2$ thỏa mãn $\left|z_1\right|+\left|z_2\right|=8$ ?

Cho hàm số $f\left(x\right)=\left|-\frac{1}{3}{x}^3+\frac{1}{2}\left(2m+3\right)x^2-\left(m^2+3m\right)x+\frac{2}{3}\right|$ . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;23] để hàm số nghịch biến trên khoảng (1;2)?

Trong không gian tọa độ Oxyz cho điểm A(-3;1-3) và đường thẳng $d:\frac{x+1}{2}=\frac{y-2}{-3}=\frac{z}{1}$ . Gọi $\left(\alpha \right)$  là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng tọa độ (Oyz). Khoảng cách từ A đến mặt phẳng $\left(\alpha \right)$  bằng

Trong các số phức z thoả mãn điều kiện $\left|z-2-5i\right|=\left|z-3i\right|$ , biết rằng $z=x+yi,$$\left(x,y\in ℝ\right)$  có môđun nhỏ nhất. Tính $P=x^2+y^2.$