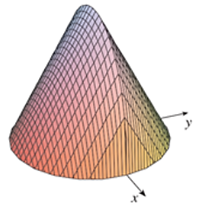
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1. Khi cắt vật thể bởi mặt phằng vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\,\,\left( { - 1 \le x \le 1} \right)\) thì được thiết diện là một tam giác đều. Thể tích \(V\) của vật thể đó là
A. \(V = \sqrt 3 .\)
B. \(V = 3\sqrt 3 .\)
 Giải bởi Vietjack
Giải bởi Vietjack
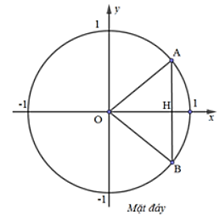
Ở mặt đáy, tam giác \[OHB\] vuông tại \(H\) nên
\(HB = \sqrt {O{B^2} - O{H^2}} = \sqrt {1 - {x^2}} \)\( \Rightarrow AB = 2\sqrt {1 - {x^2}} \).
Diện tích của mặt cắt khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\,\,\left( { - 1 \le x \le 1} \right)\) là:
\(S\left( x \right) = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{{\left( {2\sqrt {1 - {x^2}} } \right)}^2} \cdot \sqrt 3 }}{4} = \sqrt 3 \left( {1 - {x^2}} \right)\)
Thể tích \(V\) của vật thể đó là:
\[V = \int\limits_{ - 1}^1 {S\left( x \right)} \,{\rm{d}}x = \int\limits_{ - 1}^1 {\sqrt 3 \left( {1 - {x^2}} \right)} \,{\rm{d}}x = \left. {\sqrt 3 \left( {x - \frac{1}{3}{x^3}} \right)} \right|_{ - 1}^1 = \sqrt 3 \cdot \frac{4}{3} = \frac{{4\sqrt 3 }}{3}\]
Chọn C.Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Anh Tràng cứ luyên thuyên đủ chuyện trên đường đi về nhà, thị thì ngại ngùng lo lắng không biết làm sao?
Do ảnh hưởng của dịch Covid-19 nên doanh thu 6 tháng đầu năm của công ty A không đạt kế hoạch. Cụ thể, doanh thu 6 tháng đầu năm đạt 20 tỷ đồng, trong đó tháng 6 đạt 6 tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty đưa ra chỉ tiêu: kể từ tháng 7, mỗi tháng phải tăng doanh thu so với tháng kề trước \[10\% .\] Hỏi theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là bao nhiêu tỷ đồng (làm tròn đến một chữ số thập phân)?
Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức \(G\left( x \right) = 0,024{x^2}\left( {30 - x} \right)\), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp \[(x\] được tính bằng \[mg).\] Lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất là
Đọc đoạn trích sau và trả lời câu hỏi:
Còn trời đất, nhưng chẳng còn tôi mãi,
Nên bâng khuâng tôi tiếc cả đất trời;
Mùi tháng năm đều rớm vị chia phôi,
Khắp sông núi vẫn than thầm tiễn biệt...
Con gió xinh thì thào trong lá biếc,
Phải chăng hờn vì nỗi phải bay đi?
Chim rộn ràng bỗng đứt tiếng reo thi,
Phải chăng sợ độ phai tàn sắp sửa?
(Vội vàng – Xuân Diệu)
Giọng điệu chủ đạo của toàn bộ đoạn trích là gì?
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{1}{3}{x^3} - {x^2} - mx + \frac{2}{3}\) có đúng một điểm cực trị thuộc khoảng \(\left( {0\,;\,\,6} \right)\)?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tháng giêng ngon như một cặp môi gần
Tôi sung sướng. Nhưng vội vàng một nửa
Tôi không chờ nắng hạ mới hoài xuân.
(Vội vàng – Xuân Diệu)
Dòng nào dưới đây nêu đúng nhất tác dụng của dấu chấm giữa dòng trong câu thơ thứ ba.
Hỗn hợp E gồm ba ester mạch hở, đều có bốn liên kết pi (π) trong phân tử, trong đó có một ester đơn chức là ester của metacrylic acid và hai ester hai chức là đồng phân của nhau. Đốt cháy hoàn toàn 12,22 gam E bằng \({O_2}\), thu được 0,37 mol \[{H_2}O\]. Mặt khác, cho 0,36 mol E phản ứng vừa đủ với 234 ml dung dịch NaOH 2,5M, thu được hỗn hợp X gồm các muối của các acid carboxylic không no, có cùng số nguyên tử carbon trong phân tử; hai alcohol không no, đơn chức có khối lượng \({m_1}\) gam và một alcohol no, đơn chức có khối lượng \({m_2}\) gam. Tỉ lệ \({m_1}:{m_2}\)là bao nhiêu?
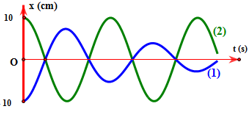
Hai chất điểm dao động có li độ phụ thuộc theo thời gian được biểu diễn tương ứng bởi hai đồ thị (1) và (2) như hình vẽ. Nhận xét nào dưới đây đúng khi nói về dao động của hai chất điểm?
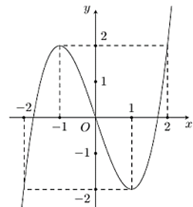
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({8^{f\left( x \right) - 2}} - 3 \cdot {4^{f\left( x \right) - 2}} + \left( {m + 3} \right){2^{f\left( x \right) - 2}} - 4 - 2m = 0\) có nghiệm \(x \in \left( { - 1\,;\,\,0} \right)?\)