Cho hình chóp \({\rm{S}}.{\rm{ABC}}\) có \({\rm{SA}}\) vuông góc với đáy, \({\rm{SA}} = 2{\rm{BC}}\) và \(\widehat {{\rm{BAC}}} = 120^\circ .\) Hình chiếu vuông góc của \({\rm{A}}\) lên các đoạn \({\rm{SB}}\) và \({\rm{SC}}\) lần lượt là \({\rm{M}}\) và \({\rm{N}}\). Góc giữa hai mặt phẳng \(\left( {{\rm{ABC}}} \right)\) và \(\left( {{\rm{AMN}}} \right)\) bằng
Giải bởi Vietjack
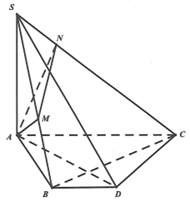
Kẻ đường kính \({\rm{AD}}\) của đường tròn ngoại tiếp \(\Delta {\rm{ABC}}\) nên \({\rm{ABD}} = {\rm{ACD}} = 90^\circ .\)
\({\rm{Ta}}\) có \(\left\{ {\begin{array}{*{20}{l}}{{\rm{BD}} \bot {\rm{BA}}}\\{{\rm{BD}} \bot {\rm{SA}}}\end{array} \Rightarrow {\rm{BD}} \bot \left( {{\rm{SAB}}} \right)} \right.\) hay \({\rm{BD}} \bot {\rm{AM}}\) và hay \({\rm{AM}} \bot \left( {{\rm{SBD}}} \right) \Rightarrow {\rm{AM}} \bot {\rm{SD}}{\rm{.}}\)
Chứng minh tương tự ta được \({\rm{AN}} \bot {\rm{SD}}\).
Suy ra \({\rm{SD}} \bot \left( {{\rm{AMN}}} \right)\), mà \({\rm{SA}} \bot \left( {{\rm{ABC}}} \right)\), \({\rm{AM}} \bot {\rm{SB}}\)
\( \Rightarrow \left( {\widehat {\left( {{\rm{ABC}}} \right),\,\,\left( {{\rm{AMN}}} \right)}} \right) = \widehat {\left( {{\rm{SA}},\,\,{\rm{SD}}} \right)} = \widehat {{\rm{DSA}}}.\)
Ta có \(BC = 2R\sin A = AD \cdot \frac{{\sqrt 3 }}{2} \Rightarrow SA = 2BC = AD\sqrt 3 \).
Vậy \(\tan \widehat {{\rm{ASD}}} = \frac{{{\rm{AD}}}}{{{\rm{SA}}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {\rm{ASD}} = 30^\circ .\) Đáp án: 30.
Tìm tất cả các giá trị của tham số \({\rm{m}}\) để hàm số \({\rm{y}} = {{\rm{x}}^4} + 4{\rm{m}}{{\rm{x}}^3} + 3(\;{\rm{m}} + 1){{\rm{x}}^2} + 1\) có cực tiểu mà không có cực đại.
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nàng rằng: Phận gái chữ tòng,
Chàng đi thiếp cũng một lòng xin đi
Từ rằng “Tâm phúc tương tri,
Sao chưa thoát khỏi nữ nhi thường tình?
Bao giờ mười vạn tinh binh,
Tiếng chiêng dậy đất bóng tinh rợp đường.
Làm cho rõ mặt phi thường,
Bấy giờ ta sẽ rước nàng nghi gia.”
(Chí khí anh hùng, trích Truyện Kiều – Nguyễn Du)
Lời của Thuý Kiều trong văn bản trên gợi nhớ đến câu nói gì theo quan niệm phong kiến?
Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá \[30\,\,000\] đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm \[1\,\,000\] đồng/kg thì số rau thừa lại tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá \[2\,\,000\] đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có thể thu lời một ngày là bao nhiêu?
Xét số phức \(z\) thỏa mãn \(\left( {{\rm{z}} + 2{\rm{i}}} \right)\left( {\overline {\rm{z}} + 2} \right)\) là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của \(z\) là một đường tròn, tâm và bán kính đường tròn có tọa độ \({\rm{I}}\left( {{\rm{a}}\,;\,\,{\rm{b}}} \right).\) Tính \(a + b.\)
Trong không gian Oxyz cho ba điểm \({\rm{A}}\left( {1\,;\,\,1\,;\,\,1} \right),\,\,{\rm{B}}\left( {5\,;\,\, - 1\,;\,\,2} \right),\,\,{\rm{C}}\left( {3\,;\,\,2\,;\,\, - 4} \right)\). Tìm tọa độ điểm \[M\] thỏa mãn \(\overrightarrow {{\rm{MA}}} + 2\overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MC}}} = \vec 0\).
Biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\left( {{x^2} + 2012} \right)\sqrt[7]{{1 - 2x}} - 2012}}{x} = \frac{a}{b}\), với \(\frac{a}{b}\) là phân số tối giản, \[a\] là số nguyên âm. Tính giá trị của \({\rm{a}} + {\rm{b}}\).
Trong không gian \({\rm{Oxyz}}\), cho điểm \({\rm{M}}\left( {4\,;\,\, - 1\,;\,\,7} \right)\), Gọi \({\rm{M'}}\) là điểm đối xứng với \({\rm{M}}\) qua trục \({\rm{Ox}}\). Khi đó, khoảng cách từ điểm \({\rm{M'}}\) đến mặt phẳng \(\left( {\rm{P}} \right):2x - 2y + z - 2 = 0\) bằng
Cho hình lăng trụ \[ABC.{\rm{ }}A'B'C'\] có đáy \({\rm{ABC}}\) là tam giác đều cạnh \({\rm{a}},\,\,{\rm{A}}A' = \frac{{3{\rm{a}}}}{2}\). Biết hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \(\left( {{\rm{ABC}}} \right)\) là trung điểm của cạnh \({\rm{BC}}\). Thể tích \({\rm{V}}\) của khối lăng trụ đó theo \(a\) là
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 1}\\{{x^2} + {y^2} = 5}\end{array}} \right.\) có bao nhiêu nghiệm?
Cho bảng số liệu:
DIỆN TÍCH GIEO TRỒNG VÀ SẢN LƯỢNG LÚA HÈ THU GIAI ĐOẠN 1990-2020
(Nguồn: gso.gov.vn)
Theo bảng số liệu, nhận xét nào sau đây là đúng về năng suất lúa hè thu của nước ta?
Phả hệ sau đây mô tả sự di truyền bệnh A và bệnh B. Biết rằng mỗi bệnh đều do 1 trong 2 alen của 1 gen quy định; các gen phân li độc lập; alen trội là trội hoàn toàn; người I.1 không mang alen gây bệnh B.
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Biểu đồ dưới đây biểu thị tốc độ tăng trưởng khách quốc tế đến Việt Nam theo tháng của năm 2018 và năm 2019.
(Nguồn: Tổng hợp số liệu từ Tổng cục thống kê)
Trong tháng nào giữa 2 năm có sự chênh lệch lớn nhất về tốc độ tăng trưởng khách quốc tế đến Việt Nam?
