Trong không gian tọa độ \({\rm{Oxyz,}}\) cho hai điểm \({\rm{A}}\left( {2\,;\,\,2\,;\,\,1} \right),\,\,{\rm{B}}\left( { - \frac{8}{3}\,;\,\,\frac{4}{3}\,;\,\,\frac{8}{3}} \right)\). Biết \({\rm{I}}\left( {{\rm{a}}\,;\,\,{\rm{b}}\,;\,\,{\rm{c}}} \right)\) là tâm đường tròn nội tiếp của tam giác \({\rm{OAB}}\). Tính \({\rm{S}} = {\rm{a}} + {\rm{b}} + {\rm{c}}\).
Giải bởi Vietjack
Ta có: \(\overrightarrow {{\rm{OA}}} = \left( {2\,;\,\,2\,;\,\,1} \right),\,\,\overrightarrow {{\rm{OB}}} = \left( { - \frac{8}{3}\,;\,\,\frac{4}{3}\,;\,\,\frac{8}{3}} \right)\)
\( \Rightarrow \overrightarrow {{\rm{OA}}} .\overrightarrow {{\rm{OB}}} = - \frac{{16}}{3} + \frac{8}{3} + \frac{8}{3} = 0 \Rightarrow \overrightarrow {{\rm{OA}}} \bot \overrightarrow {{\rm{OB}}} \)
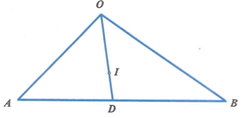
Lại có: \({\rm{OA}} = 3\,,\,\,{\rm{OB}} = 4 \Rightarrow {\rm{AB}} = 5\).Gọi \({\rm{D}}\) là chân đường phân giác trong góc \(\widehat {{\rm{AOB}}}\)\( \Rightarrow D\) thuộc đoạn \[AB.\]
Theo tính chất của phân giác trong ta có: \(\frac{{{\rm{DA}}}}{{{\rm{DB}}}} = \frac{{{\rm{OA}}}}{{{\rm{OB}}}} = \frac{3}{4} \Rightarrow \overrightarrow {{\rm{DA}}} = - \frac{3}{4}\overline {{\rm{DB}}} \Rightarrow {\rm{D}}\left( {0\,;\,\,\frac{{12}}{7}\,;\,\,\frac{{12}}{7}} \right)\).
Tam giác \({\rm{OAB}}\) có diện tích \({\rm{S}} = \frac{1}{2} \cdot {\rm{OA}} \cdot {\rm{OB}} = 6\), nửa chu vi \({\rm{p}} = \frac{{{\rm{OA}} + {\rm{OB}} + {\rm{AB}}}}{2} = 6\).
\( \Rightarrow {\rm{r}} = \frac{{\rm{S}}}{{\rm{p}}} = 1\) là bán kính đường tròn nội tiếp; chiều cao \({\rm{OH}} = \frac{{{\rm{OA}}{\rm{.OB}}}}{{{\rm{AB}}}} = \frac{{12}}{5}\).
Gọi \[I\] là tâm đường tròn nội tiếp tam giác \({\rm{OAB}}\) nên \[I\] thuộc đoạn \({\rm{OD}}\).
Ta có \(\frac{{{\rm{DI}}}}{{{\rm{DO}}}} = \frac{{\rm{r}}}{{{\rm{OH}}}} = \frac{5}{{12}} \Rightarrow \overrightarrow {{\rm{DI}}} = \frac{5}{{12}}\overrightarrow {{\rm{DO}}} \Rightarrow {\rm{I}} = \left( {0\,;\,\,1\,;\,\,1} \right)\) hay \(\left\{ {\begin{array}{*{20}{l}}{{\rm{a}} = 0}\\{\;{\rm{b}} = 1}\\{{\rm{c}} = 1}\end{array}} \right.\)
Vậy \(S = a + b + c = 2\). Chọn D.
Một vật chuyển động theo quy luật \(s = \frac{1}{3}{t^3} - {t^2} + 9t,\) với \(t\) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\] là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Có bao nhiêu giá trị nguyên của \[m \in \left( { - 10\,;\,\,10} \right)\] để hàm số \({{\rm{y}}^2}\; = {{\rm{m}}^2}{{\rm{x}}^4} - 2\left( {4\;{\rm{m}} - 1} \right){{\rm{x}}^2} + 1\) đồng biến trên khoảng \[\left( {1\,;\,\, + \infty } \right)\]?
Cho tứ diện đều \({\rm{ABCD}}\) cạnh \[a.\] Mặt phẳng \(\left( {\rm{P}} \right)\) chứa cạnh \(BC\) cắt cạnh \(AD\) tại \({\rm{E}}{\rm{.}}\) Biết góc giữa hai mặt phẳng \(\left( {\rm{P}} \right)\) và \(\left( {{\rm{BCD}}} \right)\) có số đo là \(\alpha \) thỏa mãn \(\tan \alpha = \frac{{5\sqrt 2 }}{7}.\) Gọi thể tích của hai tứ diện \({\rm{ABCE}}\) và tứ diện \({\rm{BCDE}}\) lần lượt là \({{\rm{V}}_1}\) và \({{\rm{V}}_2}\). Tính tỉ số \(\frac{{{{\rm{V}}_1}}}{{\;{{\rm{V}}_2}}}\).
Cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 2 + i\). Trên mặt phẳng \[Oxy,\] điểm biểu diễn số phức \({{\rm{z}}_1} + 2{{\rm{z}}_2}\) có tọa độ là
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f(t) = 4{t^3} - \frac{{{t^4}}}{2}\) (người). Nếu xem \(f'(t)\) là tốc độ truyền bệnh (người/ ngày) tại thời điểm \(t\) với \(t \in \left[ {0\,;\,\,6} \right]\). Hỏi vào ngày thứ mấy tốc độ truyền bệnh lớn nhất sẽ lớn nhất?
Cho hàm số \({\rm{f}}\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \({\rm{y}} = {\rm{f}}\left( {{{\rm{x}}^2} + 4{\rm{x}}} \right) - {{\rm{x}}^2} - 4{\rm{x}}\) có bao nhiêu điểm cực trị thuộc khoảng \(\left( { - 5\,;\,\,1} \right)\)?
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9. Khối chóp có thể tích lớn nhất bằng bao nhiêu?
Phương trình \(\sin 2x + 3\cos x = 0\) có bao nhiêu nghiệm trong khoảng \(\left( {0\,;\,\,\pi } \right)\)?
Cho hàm số \({\rm{f}}\left( x \right)\), hàm số \({\rm{y}} = {\rm{f'}}\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Bất phương trình \({\rm{f}}({\rm{x}}) > 2{\rm{x}} + {\rm{m}}\) \({\rm{(m}}\) là tham số thực) nghiệm đúng với mọi \(x \in \left( {0\,;\,\,2} \right)\) khi và chỉ khi
Cho số phức \(z\) thỏa mãn iz \( = 1 + 3i\). Môđun của \(z\) bằng
Xét các số phức z thỏa mãn \(\left( {\bar z + 2{\rm{i}}} \right)\left( {{\rm{z}} - 2} \right)\) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có tâm là điểm nào dưới đây?
Trong hệ tọa độ \({\rm{Oxy}}\), cho hai điểm \({\rm{A}}\left( {2\,;\,\, - 3} \right),\,\,{\rm{B}}\left( {3\,;\,\,4} \right)\). Tọa độ điểm \(M\) trên trục hoành sao cho \[A,\,\,B,\,\,M\] thẳng hàng là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
