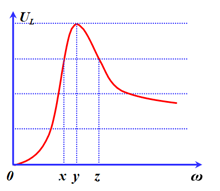
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
A. \(\frac{{{P_1} + {P_3}}}{8} = \frac{{{P_2}}}{9}.\)
Giải bởi Vietjack
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\({U_L} = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U.{Z_L}}}{R}.\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U.{Z_L}.cos\varphi }}{R} = \frac{{U.L.\omega .\cos \varphi }}{R}\) (*)
Với tần số ω1 = x và ω3 = z, cho cùng giá trị UL, ta có: \(\frac{1}{{\omega _1^2}} + \frac{1}{{\omega _3^2}} = \frac{2}{{\omega _2^2}}\)
Từ đồ thị ta thấy: \({U_{L1}} = {U_{L3}} = \frac{3}{4}{U_{L2}} = \frac{3}{4}{U_{L\max }}\)
\( \Rightarrow \frac{{U.{Z_{L1}}\cos {\varphi _1}}}{R} = \frac{{U.{Z_{L3}}\cos {\varphi _3}}}{R} = \frac{3}{4}\frac{{U.{Z_{L2}}\cos {\varphi _2}}}{R}\)
Từ (*) \( \Rightarrow \omega _1^2{\cos ^2}{\varphi _1} = \omega _3^2{\cos ^2}{\varphi _3} = \frac{9}{{16}}\omega _2^2{\cos ^2}{\varphi _2}\)
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}\frac{{\omega _2^2}}{{\omega _1^2}}}\\{\frac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}\frac{{\omega _2^2}}{{\omega _3^2}}}\end{array}} \right.\]\( \Rightarrow \frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \frac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}\omega _2^2.\left( {\frac{1}{{\omega _1^2}} + \frac{1}{{\omega _3^2}}} \right)\)
\( \Rightarrow \frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \frac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}\omega _2^2.\frac{2}{{\omega _2^2}} = \frac{9}{8}{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Công suất tiêu thụ của mạch điện là: \(P = \frac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow P\~{\cos ^2}\varphi \)
Từ (1) ta có: \(\frac{{{P_1}}}{{{P_2}}} + \frac{{{P_3}}}{{{P_2}}} = \frac{9}{8} \Rightarrow \frac{{{P_1} + {P_3}}}{9} = \frac{{{P_2}}}{8}\). Chọn B.
Cho hàm số , với \(m\) là tham số. Gọi \({m_1},\,\,{m_2}\,\,\left( {{m_1} < {m_2}} \right)\) là các giá trị của tham số \(m\) thỏa mãn \(2{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) - {\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = 8.\) Tổng \(2{m_1} + 3{m_2}\) bằng
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó \[h\left( t \right)\] là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm \(t\) giây. Chiều cao của sóng (tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng) bằng
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Hỗn hợp X gồm 2 ester đơn chức (không chứa nhóm chức nào khác). Cho 0,08 mol X tác dụng hết với dung dịch \[AgN{O_3}/N{H_3}\]thu được 0,16 mol Ag. Mặt khác thủy phân hoàn toàn 0,08 mol X bằng dung dịch NaOH dư thu được dung dịch chứa 9,34 gam hỗn hợp 2 muối và 1,6 gam \[C{H_3}OH.\]Phần trăm khối lượng ester có phân tử khối lớn hơn trong X là
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Cho hàm số \(f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = \left( {x - 1} \right)\left( {x - m} \right)\) với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số đồng biến trên \(\left( { - \infty \,;\,\, + \infty } \right)\)?
Trong không gian \[Oxyz,\] cho điểm \(H\left( {1\,;\,\,2\,;\,\, - 2} \right).\) Mặt phẳng \[\left( \alpha \right)\] đi qua \[H\] và cắt các trục \[Ox,\,\,Oy,\,\,Oz\] tại \[A,\,\,B,\,\,C\] sao cho H là trực tâm tam giác \[ABC.\] Phương trình mặt cầu tâm \(O\) và tiếp xúc với mặt phẳng \[\left( \alpha \right)\] là
Cho hàm số \(y = \frac{{x + 2}}{{2x + 3}}\) (1). Đường thẳng \(d:y = ax + b\) là tiếp tuyến của đồ thị hàm số (1). Biết \(d\) cắt trục hoành, trục tung lần lượt tại hai điểm \[A,\,\,B\] sao cho \(\Delta OAB\) cân tại \[O.\] Khi đó \(a + b\) bằng
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( {2\,;\,\, - 2\,;\,\,1} \right),\,\,B\left( {0\,;\,\,1\,;\,\,2} \right).\) Tọa độ điểm \(M\) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho ba điểm \[A,\,\,B,\,\,M\] thẳng hàng là
Số nghiệm nguyên \(x\) của thoả mãn \(\left( {{3^{{x^2} - 1}} - {{27}^{x + 1}}} \right)\left[ {{{\log }_3}\left( {x + 8} \right) - 2} \right] \le 0\) là
Gọi \(S\) là diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} + 2x - 1\) và các đường thẳng \(y = m\,,\,\,x = 0\,,\,\,x = 1.\) Để \(S \le 2021\) thì có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 4040\,;\,\, - 3} \right]?\)
Có bao nhiêu giá trị nguyên âm của tham số \(m\) để hàm số \(y = \left| {{x^5} + 2{x^4} - m{x^2} + 3x - 20} \right|\) nghịch biến trên khoảng \(\left( { - \infty \,;\,\, - 2} \right)\)?
Cho khối chóp \[S.ABC\] có \(SA \bot \left( {ABC} \right)\), tam giác ABC vuông tại \(B,\) \(AC = 2a,\) \(BC = a,\)\(SB = 2a\sqrt 3 .\) Góc giữa \[SA\] và mặt phẳng \(\left( {SBC} \right)\) là
