Thành phần biệt lập nào được sử dụng trong 2 câu thơ sau:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại.
Giải bởi Vietjack
Hai dòng thơ đầu có sử dụng các thành phần biệt lập là: Thành phần cảm thán: “Ôi”. Thành phần tình thái: “Có ngờ đâu”. Thể hiện tâm trạng xúc động rưng rưng của nhà thơ khi trở về quê cũ. Chọn B.
Một hội trường A của một trường Đại học có 600 chỗ ngồi và các hàng ghế được xếp theo dạng bậc thang, hàng ghế đầu tiên có 15 chỗ ngồi và cao \[0,3{\rm{ }}m\] so với mặt nền. Mỗi hàng ghế sau có thêm 3 chỗ ngồi và cao hơn \[0,2{\rm{ }}m\] so với hàng ghế ngay trước nó. Hỏi hàng ghế cuối cùng của hội trường đó sẽ cao bao nhiêu mét so với mặt nền?
Trong không gian \[Oxyz,\] phương trình mặt cầu đi qua điểm \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ là
Từ 180 gam glucose, bằng phương pháp lên men rượu, thu được a gam ethyl alcohol (hiệu suất 80%). Oxi hoá 0,l a gam ethyl alcohol bằng phương pháp lên men giấm, thu được hỗn hợp X. Để trung hoà hỗn hợp X cần dùng 720 ml dung dịch NaOH 0,2M. Hiệu suất quá trình lên men giấm là:
Cho hàm số Biết rằng đồ thị hàm số đã cho đi qua điểm \(\left( { - 1\,;\,\,7} \right)\) và giao điểm hai đường tiệm cận là \(\left( { - 2\,;\,\,3} \right).\) Giá trị của biểu thức \(\frac{{2a + 3b + 4c + d}}{{7c}}\) bằng\(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất \[0,65\% \] một tháng theo phương thức lãi kép. Hỏi sau bao nhiêu lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
Trong không gian \[Oxyz,\] cho hai vectơ \(\vec a = \left( {2\,;\,\,m - 1\,;\,\,3} \right)\) và \(\vec b = \left( {1\,;\,\,3\,;\,\, - 2n} \right).\) Giá trị của \[m,\,\,n\] để hai vectơ \(\vec a,\,\,\vec b\) cùng hướng với nhau là
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Hình dưới đây minh hoạ tốc độ sinh trưởng giả định của ba loài cây ngập mặn thân gỗ lâu năm kí hiệu là loài (I), (II) và (III) tương ứng với các điều kiện độ mặn khác nhau. Số liệu trong bảng dưới đây cho biết độ mặn cao nhất tại ba bãi lầy ven biển A, B và C của địa phương H. Giả sử các điều kiện sinh thái khác của ba bãi lầy này là tương đồng nhau, không ảnh hưởng đến sức sống của các loài cây này và sự sai khác về độ mặn giữa các vị trí trong mỗi bãi lầy là không đáng kể. Các cây con của ba loài này khi trồng không thể sống được ở các dải độ mặn có tốc độ sinh trưởng bằng 0.
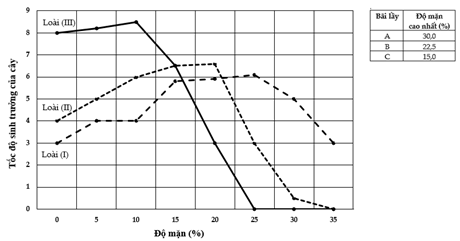
Địa phương H có kế hoạch trồng các loài cây (I), (II) và (III) để phục hồi rừng ngập mặn ở ba bãi lầy A, B và C. Dựa vào thông tin trong hình và bảng, có bao nhiêu nhận định sau đây đúng giúp địa phương H lựa chọn các loài cây này cho phù hợp?
I. Loài (I) có khả năng chịu độ mặn cao nhất trong ba loài.
II. Tốc độ sinh trưởng của loài (II) tỉ lệ nghịch với độ mặn của cả ba bãi lầy.
III. Bãi lầy B và C trồng xen được hai loài (I) và (II), bãi lầy A trồng xen được cả ba loài.
IV. Loài (III) có tốc độ sinh trưởng lớn hơn loài (I) và loài (II) ở độ mặn từ 22,5% đến 35%.
Cho hình phẳng \((H)\) được giới hạn bởi đường cong \(y = \sqrt {{m^2} - {x^2}} \) (\(m\) là tham số khác 0) và trục hoành. Khi \((H)\) quay xung quanh trục hoành được khối tròn xoay có thể tích \[V.\] Có bao nhiêu giá trị nguyên của tham số \(m\) để \(V < 1\,\,000\pi \)?
Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} - 1\) với \(a\) là tham số thực. Nếu \[{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = f\left( 1 \right)\] thì \({\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right)\) bằng
