Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 16)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 16)
-
391 lượt thi
-
156 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Cho biểu đồ:

Nhu cầu tuyển dụng lao động theo trình độ trong 6 tháng đầu năm 2018 ở trình độ nào cao nhất?
 Xem đáp án
Xem đáp án
Nhu cầu tuyển dụng lao động theo trình độ trong 6 tháng đầu năm 2018 ở trình độ lao động phổ thông là cao nhất \[\left( {66\% } \right).\] Chọn D.
Câu 2:
Trong không gian \[Oxyz,\] cho hai vectơ \(\vec a = \left( {2\,;\,\,m - 1\,;\,\,3} \right)\) và \(\vec b = \left( {1\,;\,\,3\,;\,\, - 2n} \right).\) Giá trị của \[m,\,\,n\] để hai vectơ \(\vec a,\,\,\vec b\) cùng hướng với nhau là
 Xem đáp án
Xem đáp án
Ta thấy \(\vec a\) và \(\vec b\) cùng hướng \( \Leftrightarrow \vec a = k\vec b\,\,(k > 0) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 = k}\\{m - 1 = 3k}\\{3 = k\left( { - 2n} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{k = 2}\\{m = 7\,;\,\,n = - \frac{3}{4}}\end{array}} \right.} \right..\)
Vậy \(m = 7\,;\,\,n = - \frac{3}{4}.\) Chọn A.
Câu 3:
Cho chuyển động thẳng xác định bởi phương trình \(S(t) = {t^4} - 9{t^2} - 21t\), trong đó \(t\) được tính bằng giây và \(S\) được tính bằng mét. Vận tốc của chuyển động tại thời điểm \(t = 3\) giây là
 Xem đáp án
Xem đáp án
Ta có \(v(t) = S'(t) = 4{t^3} - 18t - 21\).
Do đó, vận tốc của chuyển động tại thời điểm \(t = 3\) giây là:
\(v(3) = {4.3^3} - 18.3 - 21 = 33\,\,(\;{\rm{m}}/{\rm{s}}).\) Chọn C.
Câu 4:
 Xem đáp án
Xem đáp án
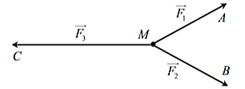
Do vật đứng yên nên tổng hợp lực tác động vào vật bằng 0.
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec 0 \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|{\rm{. }}\)
Lại có \({\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right)^2} = {\overrightarrow {{F_1}} ^2} + 2 \cdot \overrightarrow {{F_1}} \cdot \overrightarrow {{F_2}} + {\overrightarrow {{F_2}} ^2} = F_1^2 + 2 \cdot {F_1} \cdot {F_2} \cdot \cos \widehat {AMB} + F_2^2\)
Khi đó \({\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right)^2} = 2 \cdot {100^2} + 2 \cdot {100^2} \cdot \cos 60^\circ = 3 \cdot {100^2}\)\( \Leftrightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = 100\sqrt 3 {\rm{.}}\)
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = 100\sqrt 3 .\) Chọn C.
Câu 5:
Cho số phức \[z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\] thỏa mãn \(\left( {1 + i} \right)z + 2\bar z = 3 + 2i.\) Giá trị của biểu thức \(P = a + b\) là
 Xem đáp án
Xem đáp án
Ta có \(\left( {1 + i} \right)z + 2\bar z = 3 + 2i\)\( \Leftrightarrow \left( {1 + i} \right)\left( {a + bi} \right) + 2\left( {a - bi} \right) = 3 + 2i\)
\( \Leftrightarrow a + bi + ai - b + 2a - 2bi = 3 + 2i\)\( \Leftrightarrow 3a - b + \left( {a - b} \right)i = 3 + 2i\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{3a - b = 3}\\{a - b = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{1}{2}}\\{b = - \frac{3}{2}}\end{array}} \right.} \right.\).
Vậy \(P = a + b = - 1.\) Chọn D.
Câu 6:
Cho hàm số Biết rằng đồ thị hàm số đã cho đi qua điểm \(\left( { - 1\,;\,\,7} \right)\) và giao điểm hai đường tiệm cận là \(\left( { - 2\,;\,\,3} \right).\) Giá trị của biểu thức \(\frac{{2a + 3b + 4c + d}}{{7c}}\) bằng\(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
 Xem đáp án
Xem đáp án
Xét hàm số \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
Đồ thị hàm số \(f\left( x \right)\) có đường tiệm cận ngang là \(y = \frac{a}{c}.\)
Đồ thị hàm số \(f\left( x \right)\) có đường tiệm cận đứng là \(x = - \frac{d}{c}.\)
Theo bài ra, ta có: \(\left\{ {\begin{array}{*{20}{l}}{\frac{a}{c} = 3}\\{ - \frac{d}{c} = - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 3c}\\{d = 2c}\end{array}} \right.} \right.\) (1)
Điểm \(\left( { - 1\,;\,\,7} \right)\) thuộc đồ thị hàm số \(f(x) \Rightarrow \frac{{ - a + b}}{{ - c + d}} = 7\) (2)
Từ (1) và (2) suy ra \(\frac{{ - 3c + b}}{{ - c + 2c}} = 7 \Leftrightarrow b = 10c.\)
Vậy \(\frac{{2a + 3b + 4c + d}}{{7c}} = \frac{{2 \cdot (3c) + 3 \cdot (10c) + 4c + 2c}}{{7c}} = 6.\) Chọn C.
Câu 7:
Cho một hình nón có bán kính đáy bằng \(a\) và góc ở đỉnh băng \(60^\circ .\) Diện tích xung quanh của hình nón đó là
 Xem đáp án
Xem đáp án
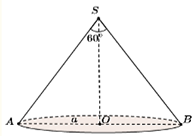
Giả sử hình nón có đỉnh là \[S,\,\,O\] là tâm của đường tròn đáy và AB là một đường kính của đáy.
\(r = OA = a\,,\,\,\widehat {ASB} = 60^\circ \Rightarrow \widehat {ASO} = 30^\circ .{\rm{ }}\)
Độ dài đường sinh là \[l = SA = \frac{{OA}}{{\sin 30^\circ }} = 2a.\]Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi \cdot a \cdot 2a = 2\pi {a^2}.\)
Chọn D.
Câu 8:
Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) cắt đường thẳng \[d:y = m\left( {x - 1} \right)\] tại ba điểm phân biệt?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của \((C)\) và \(d\) là:
\({x^3} - 3{x^2} + 2 = m\left( {x - 1} \right)\quad (1)\)
\( \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - 2} \right) = m\left( {x - 1} \right) \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - m - 2} \right) = 0\)
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 1 = 0}\\{f\left( x \right) = {x^2} - 2x - m - 2 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{f\left( x \right) = {x^2} - 2x - m - 2 = 0\,\,\,\,\,\,\,\,\,(2)}\end{array}} \right.} \right.\]
Phương trình (1) luôn có nghiệm \(x = 1\). Khi đó, để phương trình (1) luôn có ba nghiệm phân biệt thì phương trình (2) phải có hai nghiệm phân biệt khác 1.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' = 1 + m + 2 > 0}\\{f\left( 1 \right) \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 3}\\{m \ne - 3}\end{array} \Leftrightarrow m > - 3} \right.} \right.\).
Vậy \(m > - 3\) thỏa mãn yêu cầu bài toán. Chọn C.
Câu 9:
Có bao nhiêu số thực \(a\) để \(\int\limits_0^1 {\frac{x}{{a + {x^2}}}{\rm{d}}x} \; = 1\)?
 Xem đáp án
Xem đáp án
Điều kiện tích phân tồn tại là \(a + {x^2} \ne 0,\forall x \in \left[ {0\,;\,\,1} \right] \Rightarrow \left[ {\begin{array}{*{20}{l}}{a < - 1}\\{a > 0}\end{array}} \right.\)
Đặt \(t = a + {x^2} \Rightarrow dt = 2xdx.\)
Khi đó \(\int\limits_0^1 {\frac{x}{{a + {x^2}}}{\rm{d}}x} \; = \frac{1}{2}\int\limits_0^{1 + a} {\frac{{dt}}{t}} = \left. {\frac{1}{2}\left( {\ln \left| t \right|} \right)} \right|_a^{1 + a} = \frac{1}{2}\ln \left| {\frac{{1 + a}}{a}} \right| = 1\)
\( \Leftrightarrow \ln \left| {\frac{{1 + a}}{a}} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}\frac{{1 + a}}{a} = {e^2}\\\frac{{1 + a}}{a} = - {e^2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}1 + a = {e^2}a\\1 + a = - {e^2}a\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}a = \frac{1}{{{e^2} - 1}}\\a = \frac{{ - 1}}{{{e^2} + 1}}\end{array} \right.\).
So sánh điều kiện, ta có \(a = \frac{1}{{{e^2} - 1}}.\) Chọn B.
Câu 10:
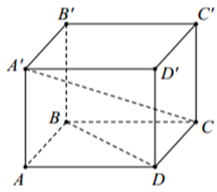
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\), biết đáy \[ABCD\] là hình vuông. Góc giữa hai đường thẳng \(A'C\) và \[BD\]bằng
 Xem đáp án
Xem đáp án
Vì \[ABCD\] là hình vuông nên \(BD \bot AC.\)
Mặt khác \(AA' \bot \left( {ABCD} \right) \Rightarrow BD \bot AA'.\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{BD \bot AA'}\end{array} \Rightarrow BD \bot \left( {AA'C} \right) \Rightarrow BD \bot A'C} \right..\)
Do đó, góc giữa \(A'C\) và BD bằng \(90^\circ .\) Chọn A.
Câu 11:
Biết tập nghiệm của bất phương trình \(\left( {{x^2} + 2x - 8} \right)\sqrt {16 - {x^2}} \le 0\) có dạng \(S = \left[ { - a\,;\,\,b} \right] \cup \left\{ c \right\}\) với \[a,\,\,b,\,\,c\] là các số nguyên dương. Giá trị biểu thức \(P = 2a - b + 3c\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\left( {{x^2} + 2x - 8} \right)\sqrt {16 - {x^2}} \le 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{16 - {x^2} = 0}\\{\left\{ {\begin{array}{*{20}{l}}{16 - {x^2} > 0}\\{{x^2} + 2x - 8 \le 0}\end{array}} \right.}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \pm 4}\\{\left\{ {\begin{array}{*{20}{l}}{ - 4 < x < 4}\\{ - 4 \le x \le 2}\end{array}} \right.}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \pm 4}\\{ - 4 < x \le 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 4}\\{ - 4 \le x \le 2}\end{array}} \right.} \right.\).
Do đó, tập nghiệm của bất phương trình là \(S = \left[ { - 4\,;\,\,2} \right] \cup \left\{ 4 \right\}.\)
Suy ra \(a = 4,\,\,b = 2,\,\,c = 4.\)
Vậy \(P = 2.4 - 2 + 3.4 = 18.\) Chọn C.
Câu 12:
Trong không gian \[Oxyz,\] cho bốn điểm \[A\left( {1\,;\,\, - 2\,;\,\,0} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right),\]\[C\left( { - 2\,;\,\,1\,;\,\,3} \right),\]\[D\left( {0\,;\,\,1\,;\,\,1} \right)\]. Thể tích khối tứ diện \[ABCD\] bằng
 Xem đáp án
Xem đáp án
Ta có: \(\overrightarrow {AB} = \left( {1\,;\,\,2\,;\,\,3} \right)\,;\,\,\overrightarrow {AC} = \left( { - 3\,;\,\,3\,;\,\,3} \right)\,;\,\,\overrightarrow {AD} = \left( { - 1\,;\,\,3\,;\,\,1} \right)\).
\(\left[ {\overrightarrow {AB} \,,\,\,\overrightarrow {AC} } \right] = \left( { - 3\,;\,\, - 12\,;\,\,9} \right)\) ; \(\left[ {\overrightarrow {AB} \,,\,\,\overrightarrow {AC} } \right] \cdot \overrightarrow {AD} = \left( { - 3} \right) \cdot \left( { - 1} \right) + \left( { - 12} \right) \cdot 3 + 9 \cdot 1 = - 24\).
Do đó \({V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} \,,\,\,\overrightarrow {AC} } \right] \cdot \overrightarrow {AD} } \right| = \frac{1}{6}\left| { - 24} \right| = 4\). Chọn D.
Câu 13:
Một hội trường A của một trường Đại học có 600 chỗ ngồi và các hàng ghế được xếp theo dạng bậc thang, hàng ghế đầu tiên có 15 chỗ ngồi và cao \[0,3{\rm{ }}m\] so với mặt nền. Mỗi hàng ghế sau có thêm 3 chỗ ngồi và cao hơn \[0,2{\rm{ }}m\] so với hàng ghế ngay trước nó. Hỏi hàng ghế cuối cùng của hội trường đó sẽ cao bao nhiêu mét so với mặt nền?
 Xem đáp án
Xem đáp án
Hàng ghế đầu tiên có 15 chỗ ngồi và cao \[0,3{\rm{ }}m\] so với mặt nền.
Hàng ghế thứ hai có 18 chỗ ngồi và cao \[0,5{\rm{ }}m\] so với mặt nền.
Hàng ghế thứ hai có 21 chỗ ngồi và cao \[0,7{\rm{ }}m\] so với mặt nền.
.....
Dễ thấy, số ghế ngồi và độ cao của hàng ghế lập thành các cấp số cộng.
Xét số ghế ngồi: \({u_1} = 15\) và công sai \(d = 3\) nên \({S_n} = \frac{{[30 + 3(n - 1)] \cdot n}}{2} = 600\).
Suy ra \(3{n^2} + 27n - 1\,\,200 = 0 \Leftrightarrow n = 16\) (số nguyên dương).
Xét độ cao của các hàng ghế: \({u_1} = 0,3\) và \(d = 0,2\).
Suy ra hàng ghế cuối cùng cao so với mặt nền là \({u_{16}} = 0,3 + 15 \cdot 0,2 = 3,3\,\,(m).\)
Chọn D.
Câu 14:
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 1}\\{{x^2} + 3{y^2} = 7}\end{array}} \right.\) có nghiệm là \(\left( {{x_0};{y_0}} \right)\) với \({x_0} > 0.\) Giá trị của biểu thức \(P = {x_0} + 2{y_0}\) bằng
 Xem đáp án
Xem đáp án
Từ phương trình \(x + y = 1\) ta rút \(y = 1 - x\) thế vào phương trình \({x^2} + 3{y^2} = 7\) ta được:
\[{x^2} + 3{\left( {1 - x} \right)^2} = 7 \Leftrightarrow 4{x^2} - 6x - 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = - \frac{1}{2}}\end{array}} \right.\].
Vì \({x_0} > 0\) nên chọn \({x_0} = 2 \Rightarrow {y_0} = - 1.\)
Vậy \(P = {x_0} + 2{y_0} = 0.\) Chọn C.
Câu 15:
Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất \[0,65\% \] một tháng theo phương thức lãi kép. Hỏi sau bao nhiêu lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
 Xem đáp án
Xem đáp án
Áp dụng công thức lãi kép, ta được \[20 \cdot {\left( {1 + 0,65\% } \right)^n} - 20 > 20\]
\( \Leftrightarrow {\left( {1 + 0,65\% } \right)^n} > 2 \Leftrightarrow 1,{0065^n} > 2 \Leftrightarrow n > {\log _{1,0065}}2 \approx 107\) (tháng).
Vậy sau 8 năm 11 tháng thì vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng. Chọn A.
Câu 16:
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}\)?
 Xem đáp án
Xem đáp án
Xét hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\)
\( \Rightarrow y' = m{x^2} - 4mx + 3m + 5\).
Trường hợp 1: \(a = 0 \Leftrightarrow m = 0 \Rightarrow y' = 5 > 0 \Rightarrow \) Hàm số đồng biến trên \(\mathbb{R}\).
Trường hợp 2: \(a \ne 0 \Leftrightarrow m \ne 0\).
Hàm số đã cho đồng biến trên \(\mathbb{R}\) khi và chỉ khi \(y' \ge 0,\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{\left( {2m} \right)^2} - m\left( {3m + 5} \right) \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{m^2} - 5m \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\0 \le m \le 5\end{array} \right.\)\( \Leftrightarrow 0 < m \le 5.\)
Vì \[m \in \mathbb{Z} \Rightarrow m \in \left\{ {0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5} \right\}.\] Chọn D.
Câu 17:
Trên mặt phẳng hệ tọa độ \[Oxy,\] cho điểm \(I\left( {1\,;\,\, - 1} \right)\) và hai đường thẳng \({d_1}:x + y - 3 = 0,\) \({d_2}:x - 2y - 6 = 0.\) Hai điểm \[A,\,\,B\] lần lượt thuộc hai đường thẳng \({d_1},\,\,{d_2}\) sao cho \(I\) là trung điểm của đoạn thẳng AB. Đường thẳng \[AB\] có một vectơ chỉ phương là
 Xem đáp án
Xem đáp án
Vì \(A \in {d_1}\), \(B \in {d_2}\) nên gọi \[A\left( {a\,;\,\,3 - a} \right)\]; \(B\left( {2b + 6\,;\,\,b} \right).\)
Vì \(I\) là trung điểm của đoạn thẳng \(AB\) nên \(\left\{ {\begin{array}{*{20}{l}}{\frac{{a + 2b + 6}}{2} = 1}\\{\frac{{3 - a + b}}{2} = - 1}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + 2b = - 4}\\{a - b = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 3}\end{array}} \right.} \right.\)
\( \Rightarrow A\left( {2\,;\,\,1} \right)\,;\,\,B\left( {0\,;\,\, - 3} \right) \Rightarrow \overrightarrow {BA} = \left( {2\,;\,\,4} \right) \Rightarrow \overrightarrow {BA} = 2 \cdot {\vec u_1}.\)
Vậy đường thẳng \[AB\] có một vectơ chỉ phương là \({\vec u_1} = \left( {1\,;\,\,2} \right).\) Chọn A.
Câu 18:
Cho hình phẳng \((H)\) được giới hạn bởi đường cong \(y = \sqrt {{m^2} - {x^2}} \) (\(m\) là tham số khác 0) và trục hoành. Khi \((H)\) quay xung quanh trục hoành được khối tròn xoay có thể tích \[V.\] Có bao nhiêu giá trị nguyên của tham số \(m\) để \(V < 1\,\,000\pi \)?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đường cong và trục hoành là: \(\sqrt {{m^2} - {x^2}} = 0 \Leftrightarrow x = \pm \,m.\)
Thể tích vật thể tròn xoay cần tính là:
\[V = \pi \int\limits_{ - \left| m \right|}^{\left| m \right|} {\left( {{m^2} - {x^2}} \right)} \,dx = \left. {\pi \left( {{m^2}x - \frac{1}{3}{x^3}} \right)} \right|_{ - \left| m \right|}^{\left| m \right|} = \frac{{4\pi {m^2}\left| m \right|}}{3}.\]
Ta có: \(V < 1\,\,000\pi \Leftrightarrow \frac{{4\pi {m^2}\left| m \right|}}{3} < 1\,\,000\pi \Leftrightarrow {\left| m \right|^3} < 750 \Leftrightarrow - \sqrt[3]{{750}} < m < \sqrt[3]{{750}}.\)
Vậy với \(m \ne 0\) thì có 18 giá trị nguyên của \(m\) thỏa mãn yêu cầu đề bài.
Chọn A.
Câu 19:
Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là
 Xem đáp án
Xem đáp án
Câu 20:
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều, \(SA \bot \left( {ABC} \right).\) Mặt phẳng \(\left( {SBC} \right)\) cách \(A\) một khoảng bằng \(a\) và hợp với mặt phẳng \(\left( {ABC} \right)\) góc \(30^\circ .\) Thể tích của khối chóp \[S.ABC\] bằng
 Xem đáp án
Xem đáp án
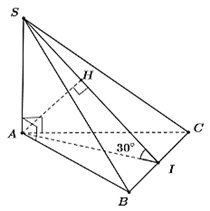
Gọi \(I\) là trung điểm của BC suy ra \(AI \bot BC\) tại I.
Ta có \(SA \bot BC \Rightarrow (SAI) \bot BC \Rightarrow SI \bot BC.\)
\( \Rightarrow \left( {\widehat {\left( {SBC} \right),\,\,\left( {ABC} \right)}} \right) = \widehat {SIA} = 30^\circ .\)
Vì \(H\) là hình chiếu vuông góc của \(A\) trên \(SI,\) \(AH \subset (SAI) \Rightarrow AH \bot BC \Rightarrow d\left( {A,\,\,\left( {SBC} \right)} \right) = AH = a.\)
• Xét tam giác AHI vuông tại \(H\) suy ra \(AI = \frac{{AH}}{{\sin 30^\circ }} = 2a.\)Giả sử tam giác đều \[ABC\] có cạnh bằng \(x\), mà \[AI\] là đường cao.
• Xét tam giác \[ABI\] vuông tại \(I\) suy ra: \(x = AB = \frac{{AI}}{{\cos 30^\circ }} = \frac{{4a}}{{\sqrt 3 }}.\)
Diện tích tam giác đều \[ABC\] là: \({S_{ABC}} = \frac{1}{2} \cdot 2a \cdot \frac{{4a}}{{\sqrt 3 }} = \frac{{4{a^2}\sqrt 3 }}{3}.\)
• Xét tam giác \[SAI\] vuông tại \(A\) suy ra \(SA = AI \cdot \tan 30^\circ = \frac{{2a}}{{\sqrt 3 }}.\)
Vậy \({V_{S.ABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot SA = \frac{1}{3} \cdot \frac{{4{a^2}\sqrt 3 }}{3} \cdot \frac{{2a}}{{\sqrt 3 }} = \frac{{8{a^3}}}{9}.\) Chọn A.Câu 21:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 1} \right)^2}\left( {x + 2} \right){\left( {x - 3} \right)^3}\) với mọi \(x \in \mathbb{R}.\) Hàm số \(y = f\left( x \right)\) có
 Xem đáp án
Xem đáp án

Vậy hàm số đã cho có 1 điểm cực đại và 2 điểm cực tiểu. Chọn A.
Câu 22:
Có bao nhiêu cặp số dương \(\left( {a\,;\,\,b} \right)\) thỏa mãn \({\log _2}a\) là số nguyên dương, \({\log _2}a = 1 + {\log _3}b\) và \({a^2} + {b^2} < {2020^2}\)?
 Xem đáp án
Xem đáp án
Vì \({a^2} + {b^2} < {2020^2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a < 2020}\\{b < 2020}\end{array}} \right..\)
Ta có \({\log _2}a = 1 + {\log _3}b < 1 + {\log _3}2020.\)
Vì \({\log _2}a\) là số nguyên dương nên \({\log _2}a \in \left\{ {1\,;\,\,2\,;\,\, \ldots \,;\,\,7} \right\}\)
Khi đó \(a\) có thể nhận 7 giá trị.
Lại có \(b = {3^{{{\log }_2}a - 1}}\) nên với mỗi giá trị của \(a\) thỏa mãn sẽ tương ứng với một giá trị của \(b\) nếu thỏa mãn điều kiện.
Thử lại: Với \({\log _2}a = 7 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = {2^7}}\\{b = {3^6}}\end{array} \Rightarrow {a^2} + {b^2} < {{2020}^2}} \right.\) (thỏa mãn).
Vậy có tất cả 7 cặp số thực dương \[\left( {a\,;\,b} \right)\] thỏa mãn. Chọn C.
Câu 23:
 Xem đáp án
Xem đáp án
Với \(\forall x \in \left( {1\,;\,\, + \infty } \right)\) ta có \(f\left( x \right) = \int {\left( {\frac{1}{{x - 1}} + 6x} \right)dx} = \ln \left( {x - 1} \right) + 3{x^2} + C.\)
Vì \(f\left( 2 \right) = 12 \Rightarrow C = 0 \Rightarrow f\left( x \right) = \ln \left( {x - 1} \right) + 3{x^2}.\)
\(F\left( x \right) = \int {\left( {\ln (x - 1) + 3{x^2}} \right)dx} = x\ln \left( {x - 1} \right) - \int x d\left( {\ln \left( {x - 1} \right)} \right) + {x^3}\)
\( = x\ln dx - \int x \cdot \frac{1}{{x - 1}}dx + {x^3}\)\[ = x\ln \left( {x - 1} \right) - x - \ln \left( {x - 1} \right) + {x^3} + C' \cdot F(2) = 6\] nên \(C' = 0.\)
Suy ra \(F\left( x \right) = x\ln \left( {x - 1} \right) - x - \ln \left( {x - 1} \right) + {x^3}.\)
\(P = F\left( 5 \right) - 4F\left( 3 \right) = 5\ln 4 - 5 - \ln 4 + 125 - 4\left( {3\ln 2 - 3 - \ln 2 + 27} \right) = 120 - 96 = 24.{\rm{ }}\)
Chọn D.
Câu 24:
Cho hình trụ có bán kính đáy bằng 3. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
 Xem đáp án
Xem đáp án
Vì thiết diện qua trục của hình trụ là hình vuông nên suy ra \(h = 2R = 6\).
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh = 2\pi .3.6 = 36\pi .\)
Chọn B.
Câu 25:
Trong không gian \[Oxyz,\] phương trình mặt cầu đi qua điểm \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ là
 Xem đáp án
Xem đáp án
Gọi \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm của mặt cầu \((S).\)
Mặt cầu \((S)\) tiếp xúc với các mặt phẳng tọa độ
\[ \Rightarrow d\left( {I,\,\,\left( {Oxy} \right)} \right) = d\left( {I,\,\,\left( {Oyz} \right)} \right) = d\left( {I,\,\,\left( {Oxz} \right)} \right) \Leftrightarrow \left| a \right| = \left| b \right| = \left| c \right| = R\].
Mặt cầu \((S)\) đi qua \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ.
Suy ra \(I\) và \(A\) phải cùng nằm trên một góc phần tám.
\( \Rightarrow \left\{ \begin{array}{l}IA = R\\a > 0\,;\,\,c > 0\,;\,\,b < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}I{A^2} = {R^2}\\a > 0\,;\,\,c > 0\,;\,\,b < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {a - 1} \right)}^2} + {{\left( {b + 1} \right)}^2} + {{\left( {c - 4} \right)}^2} = {R^2}}\\{a = c = - b = R > 0\,\,\,\,\,\,\,\,\,(do\,\,(1))}\end{array}} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {a - 1} \right)^2} + {\left( { - a + 1} \right)^2} + {\left( {a - 4} \right)^2} = {a^2}\\a = c = - b = R > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{a^2} - 12a + 18 = 0\\a = c = - b = R > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 6a + 9 = 0\\a = c = - b = R > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = c = 3\\b = - 3\\R = 3\end{array} \right..\)
Do đó \(\left( S \right):{\left( {x - 3} \right)^3} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 9.\) Chọn B.
Câu 26:
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20\,;\,\,20} \right]\) để hàm số \(y = - {x^4} + 6{x^2} + \left( {m - 2} \right)x + 3\) có đúng một điểm cực trị?
 Xem đáp án
Xem đáp án
Ta có \(y' = - 4{x^3} + 12x + m - 2\).
Suy ra \(y' = 0 \Leftrightarrow m = 4{x^3} - 12x + 2 = f\left( x \right).\)
Yêu cầu bài toán \( \Leftrightarrow m = f\left( x \right)\) có đúng một nghiệm đơn
Hoặc có 2 nghiệm gồm một nghiệm đơn và một nghiệm kép.
Dựa vào BBT của \(f\left( x \right) \Rightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 10}\\{m \le - 6}\end{array}} \right.\) mà \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 20\,;\,\,20} \right]\).
Do đó có \(\left( {20 - 10 + 1} \right) + \left( { - 6 + 20 + 1} \right) = 26\) giá trị nguyên cần tìm. Chọn B.
Câu 27:
 Xem đáp án
Xem đáp án
ĐKХĐ: \(x > 0\,;\,\,{3^x} - 3 \cdot {2^{x - 1}} \ge 0\)
• TH1: \({3^x} - {3.2^{x - 1}} = 0 \Leftrightarrow {3^x} = \frac{3}{2}{.2^x} \Leftrightarrow {\left( {\frac{3}{2}} \right)^x} = \frac{3}{2} \Leftrightarrow x = 1\) (thỏa mãn)
• TH2: \(\left\{ {\begin{array}{*{20}{l}}{{3^x} - {{3.2}^{x - 1}} > 0}\\{\log _2^2\left( {4x} \right) - 3{{\log }_{\sqrt 2 }}x - 7 \le 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 1}\\{{{\left( {2 + {{\log }_2}x} \right)}^2} - 6{{\log }_2}x - 7 \le 0}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 1}\\{ \log _2^2x - 2 {{\log }_2}x - 3 \le 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 1}\\{ - 1 \le {{\log }_2}x \le 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 1}\\{\frac{1}{2} \le x \le 8}\end{array} \Leftrightarrow 1 < x \le 8.} \right.} \right.} \right.\)
Từ hai trường hợp, ta suy ra \[x \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\, \ldots \,;\,\,8} \right\}.\]
Vậy có 8 số nguyên \(x\) thỏa mãn đề bài. Chọn A.
Câu 28:
Cho hình chóp tứ giác đều \[S.ABCD\] có tất cả các cạnh bằng 1. Gọi \[G\] là trọng tâm của tam giác \[SBC.\] Thể tích khối tứ diện \[SGCD\] bằng
 Xem đáp án
Xem đáp án
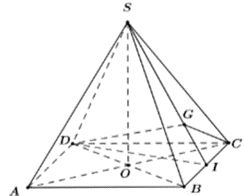
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\) (vì \[S.ABCD\] là hình chóp tứ giác đều).
Gọi \(I\) là trung điểm cạnh \[BC.\]
• Xét hình vuông \[ABCD\] có: \(OC = \frac{1}{2}AC = \frac{1}{2} \cdot \sqrt {{1^2} + {1^2}} = \frac{{\sqrt 2 }}{2}\)
• Xét \[\Delta SOC\] vuông tại \(O\) có \(SO = \sqrt {S{C^2} - O{C^2}} = \frac{{{{\sqrt 2 }^2}}}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{{\sqrt 2 }}{6}.\)Ta có \({V_{S.DCI}} = \frac{1}{2}{V_{S.DBC}} = \frac{1}{2} \cdot \frac{1}{2}{V_{S.ABCD}} = \frac{{\sqrt 2 }}{{24}}\) (vì \({S_{DBC}} = \frac{1}{2}{S_{ABCD}}\) và \(\left. {IC = \frac{1}{2}BC} \right).\)
\(\frac{{{S_{S.DCG}}}}{{{S_{S.DCI}}}} = \frac{{SD}}{{SD}} \cdot \frac{{SC}}{{SC}} \cdot \frac{{SG}}{{SI}} = \frac{2}{3}\) (vì \(G\) là trọng tâm tam giác \(SBC).\)
\( \Rightarrow {V_{S.DCG}} = \frac{2}{3}{V_{S.DCI}} = \frac{2}{3} \cdot \frac{{\sqrt 2 }}{{24}} = \frac{{\sqrt 2 }}{{36}}.\) Chọn A.
Câu 29:
Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} - 1\) với \(a\) là tham số thực. Nếu \[{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = f\left( 1 \right)\] thì \({\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right)\) bằng
 Xem đáp án
Xem đáp án
Ta có \({\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = f\left( 1 \right) \Rightarrow f'\left( 1 \right) = 0.\)
\(f'\left( x \right) = 4a{x^3} + 4\left( {a + 4} \right)x \Rightarrow f'\left( 1 \right) = 4a + 4\left( {a + 4} \right) = 8a + 16\).
Do đó \(f'\left( 1 \right) = 0 \Leftrightarrow 8a + 16 = 0 \Leftrightarrow a = - 2.\)
Suy ra \(f\left( x \right) = - 2{x^4} + 4{x^2} - 1 \Rightarrow {\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = - 17.\) Chọn D.
Câu 30:
Trong không gian \[Oxyz,\] cho điểm \(M\left( {3\,;\,\,2\,;\,\,1} \right).\) Mặt phẳng \((P)\) đi qua \(M\) và cắt các trục tọa độ \[Ox,\,\,Oy,\,\,Oz\] lần lượt tại các điểm \[A,\,\,B,\,\,C\] không trùng với gốc tọa độ sao cho \(M\) là trực tâm tam giác \[ABC.\] Mặt phẳng nào dưới đây song song với \((P)\)?
 Xem đáp án
Xem đáp án
Gọi \[A\left( {a\,;\,\,0\,;\,\,0} \right),\,\,B\left( {0\,;\,\,b\,;\,\,0} \right),\,\,C\left( {0\,;\,\,0\,;\,\,c} \right)\]
Phương trình mặt phẳng \((P)\) có dạng: \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1(a.b.c \ne 0)\)
Vì \(M \in (P)\) nên \(\frac{3}{a} + \frac{2}{b} + \frac{1}{c} = 1\).
Ta có: \[\overrightarrow {MA} = \left( {a - 3\,;\,\, - 2\,;\,\, - 1} \right),\,\,\overrightarrow {MB} = \left( { - 3\,;\,\,b - 2\,;\,\, - 1} \right),\,\,\overrightarrow {BC} = \left( {0\,;\,\, - b\,;\,\,c} \right),\,\,\overrightarrow {AC} = \left( { - a\,;\,\,0\,;\,\,c} \right).\]
Vì \(M\) là trực tâm tam giác ABC nên: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MA} \cdot \overrightarrow {BC} = 0}\\{\overrightarrow {MB} \cdot \overrightarrow {AC} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2b - c = 0}\\{3a - c = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2b = c}\\{3a = c}\end{array}} \right.} \right.} \right.\)
Tử (1) và (2) suy ra \(a = \frac{{14}}{3}\,;\,\,b = \frac{{14}}{2}\,;\,\,c = 14.\)
Khi đó phương trình \((P):3x + 2y + z - 14 = 0\).
Vật mặt phẳng song song với \((P)\) là: \(3x + 2y + z + 14 = 0.\) Chọn A.
Câu 31:
 Xem đáp án
Xem đáp án
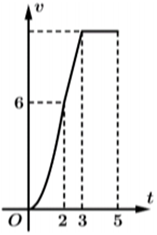
Trong 2 giây đầu \({v_1} = a{t^2}\), lại có \(t = 2\,s \Rightarrow {v_1} = 60\,\,{\rm{m}}/{\rm{s}}\)
Nên \(60 = a \cdot {2^2} \Leftrightarrow a = 15\) suy ra \({v_1} = 15{t^2}.\)
Quãng đường vật đi được trong 2 giây đầu là \({s_1} = \int\limits_0^2 {{v_1}\left( t \right){\rm{d}}t} = \int\limits_0^2 {15{t^2}{\rm{d}}t} = 40\,\,(m).\)
Trong giây tiếp theo, thì vận tốc là \({v_2} = mt + n\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{t = 2 \Rightarrow v = 60\,\,(\;{\rm{m}}/{\rm{s}})}\\{t = 3 \Rightarrow v = 100\,\,(\;{\rm{m}}/{\rm{s}})}\end{array}} \right.\)
Khi đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2m + n = 60}\\{3m + n = 100}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = 40}\\{n = - 20}\end{array}} \right.} \right.\) \( \Rightarrow {v_2}\left( t \right) = 40t - 20.\)
Quãng đường vật đi được trong giây tiếp theo là: \[{s_2} = \int\limits_2^3 {{v_2}\left( t \right){\rm{d}}t} = \int\limits_2^3 {\left( {40t - 20} \right){\rm{d}}t} \].
Trong 2 giây cuối, \({v_3} = 100\,\,\;{\rm{m}}/{\rm{s}}\).
Quãng đường vật đi được trong 2 giây cuối là: \({s_3} = \int\limits_3^5 {{v_3}\left( t \right)dt} = \int\limits_3^5 {100dt} = 200\,\,(m).\)
Vậy trong 5 giây đó xe đã đi được quãng đường là: \(40 + 80 + 200 = 320\,\,(\;{\rm{m}}).\) Chọn D.
Câu 32:
Cho hàm số \(y = {x^3} + 3{x^2} + 1\) có đồ thị \(\left( C \right)\) và điểm \(A\left( {1\,;\,\,m} \right).\) Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để qua \(A\) có thể kẻ được đúng ba tiếp tuyến tới đồ thị \(\left( C \right).\) Số phần tử của \(S\) là
 Xem đáp án
Xem đáp án
Gọi \(k\) là hệ số góc của đường thẳng \(d\) qua A.
Ta có phương trình của \(d\) có dạng: \[y = k\left( {x - 1} \right) + m = kx + m - k.\]
\(d\) tiếp xúc \((C) \Leftrightarrow \) hệ sau có nghiệm \(\left\{ {\begin{array}{*{20}{l}}{kx + m - k = {x^3} + 3{x^2} + 1}\\{k = 3{x^2} + 6x}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = - 2{x^3} + 6x + 1}\\{k = 3{x^2} + 6x}\end{array}} \right.} \right..\)
Yêu cầu bài toán \( \Leftrightarrow \) phương trình \((*)\) phải có 3 nghiệm phân biệt.
Xét hàm số \(f\left( x \right) = - 2{x^3} + 6x + 1\); Ta có \(f'\left( x \right) = - 6{x^2} + 6 = 0 \Leftrightarrow x = \pm 1.\)
Ta có bảng biến thiên:
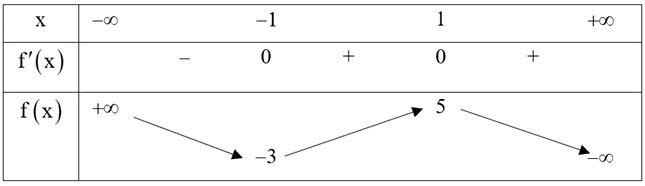
Từ bảng biến thiên, để phương trình \((*)\) có 3 nghiệm phân biệt suy ra \( - 3 < m < 5.\)
Vậy số phần tử của \(S\) là 7. Chọn B.
Câu 33:
Trong không gian \[Oxyz,\] cho mặt phẳng \(\left( P \right):x + y - z - 1 = 0.\) Đường thẳng \(d\) đi qua \(O,\) song song với \(\left( P \right)\) đồng thời vuông góc với Oz có một vectơ chỉ phương là \(\vec u = \left( {a\,;\,\,1\,;\,\,b} \right).\) Tính \(a - b.\)
 Xem đáp án
Xem đáp án
Ta có \(d\,{\rm{//}}\,\left( P \right) \Rightarrow {\vec u_d} \bot {\vec n_{\left( P \right)}}\left( {1\,;\,\,1\,;\,\, - 1} \right)\).
Lại có \(d \bot Oz \Rightarrow {\vec u_d} \bot {\vec u_{Oz}}\left( {0\,;\,\,0\,;\,\,1} \right)\)
Do đó \[{\vec u_d} = \left[ {{{\vec n}_{\left( P \right)}};\,\,{{\vec u}_{Oz}}} \right] = \left( {1\,;\,\, - 1\,;\,\,0} \right)\,{\rm{//}}\,\left( { - 1\,;\,\,1\,;\,\,0} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 0}\end{array}} \right..\] Chọn D.
Câu 34:
 Xem đáp án
Xem đáp án
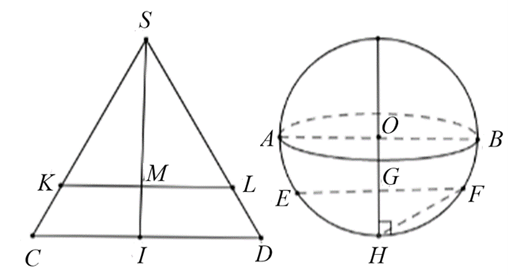
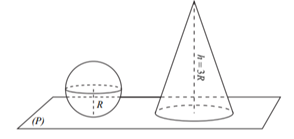
Gọi \(G\) là tâm của thiết diện cắt bởi mặt phẳng \(\left( Q \right)\) và mặt cầu.
Theo giả thiết ta có \(OA = OB = OH = R = 5\) và \(HG = x.\)
GF là bán kính của đường tròn thiết diện. Khi đó \(GF = \sqrt {{5^2} - {{(5 - x)}^2}} = \sqrt {10x - {x^2}} .\)
Gọi \({S_1}\) là tâm của thiết diện cắt bởi mặt phẳng \((Q)\) và mặt cầu.
Gọi \(M\) là tâm của thiết diện cắt bởi \((Q)\) và hình nón.
Theo giả thiết ta có \(MI = x\) và \(\frac{{SM}}{{SI}} = \frac{{ML}}{{ID}} \Rightarrow ML = \frac{{SM \cdot ID}}{{SI}} = \frac{{\left( {15 - x} \right) \cdot 5}}{{15}} = 5 - \frac{x}{3}{\rm{. }}\)
Gọi \({S_2}\) là diện tích thiết diện của mặt phẳng \((Q)\) và hình nón. Ta có \({S_2} = \pi {\left( {5 - \frac{x}{3}} \right)^2}\)
Do đó \(S = {S_1} + {S_2} = \pi \left[ {10x - {x^2} + {{\left( {5 - \frac{x}{3}} \right)}^2}} \right] = \pi \left( { - \frac{8}{9}{x^2} + \frac{{20}}{3}x + 25} \right)\)
Ta có \(S\) đạt giá trị lớn nhất khi \(f(x) = - \frac{8}{9}{x^2} + \frac{{20}}{3}x + 25\) đạt giá trị lớn nhất \( \Leftrightarrow x = \frac{{15}}{4}.\)
Theo đề ra ta có: \(x = \frac{a}{b} = \frac{{15}}{4} \Rightarrow T = a + b = 19.\) Chọn B.
Câu 35:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 36:
Gọi \[S\] là tập hợp các số tự nhiên có 9 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số từ tập \[S.\] Xác suất để số được chọn có đúng bốn chữ số lẻ sao cho chữ số 0 luôn đứng giữa hai chữ số lẻ bằng
 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 37:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 38:
Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? (Biết rằng có 4 học sinh của nhóm không tham gia tiết mục nào).
 Xem đáp án
Xem đáp án
Kí hiệu A là tập hợp học sinh tham gia tiết mục múa, B là tập hợp học sinh tham gia tiết mục hát, E là tập hợp nhóm học sinh.
Ta có thể biểu diễn tập hợp đó bằng biểu đồ Ven:
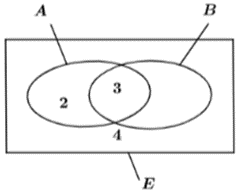
Khi đó, \(A \cap B\) là tập hợp học sinh tham gia cả hai tiết mục.
Số phần tử của tập hợp A là 5, số phần tử của tập hợp \(A \cap B\) là 3, số phần tử của tập hợp E là 12.
Số học sinh tham gia ít nhất một trong hai tiết mục là: \(12 - 4 = 8\) (học sinh).
Số học sinh tham gia tiết mục hát mà không tham gia tiết mục múa là: \(8 - 5 = 3\) (học sinh).
Số học sinh tham gia tiết mục hát là: \(3 + 3 = 6\) (học sinh).
Đáp án: 6.
Câu 39:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 40:
Cho dãy số \[\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{l}}{{u_1} = - 1}\\{{u_{n + 1}} = {u_n} + 3}\end{array}\,\,\left( {\forall n \in \mathbb{N},\,\,n \ge 1} \right)} \right..\] Tính \(\lim \frac{{{u_n}}}{{5n + 2020}}.\)
 Xem đáp án
Xem đáp án
Ta có \(\left( {{u_n}} \right)\) là cấp số cộng có \({u_1} = - 1,d = 3,{u_n} = {u_1} + (n - 1)d = - 1 + (n - 1).3 = 3n - 4.\)
\( \Rightarrow \lim \frac{{{u_n}}}{{5n + 2020}} = \lim \frac{{3n - 4}}{{5n + 2020}} = \lim \frac{{3 - \frac{4}{n}}}{{5 + \frac{{2020}}{n}}} = \frac{3}{5}{\rm{. }}\)
Đáp án: \(\frac{3}{5}.\)
Câu 41:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 42:
Cho hình nón có chiều cao \(h = 20\), bán kính đáy \(r = 25.\) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12. Tính diện tích \(S\) của thiết diện đó.
 Xem đáp án
Xem đáp án
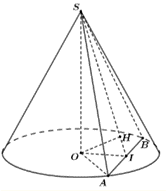
Giả sử nón đỉnh \(S\), tâm đáy \(O\) và có thiết diện qua đỉnh thỏa mãn yêu cầu bài toán là \(\Delta SAB.\)
Ta có \[SO\] là đường cao của hình nón nên \(SO \bot AB.\)
Gọi \(I\) là trung điểm của \(AB \Rightarrow OI \bot AB.\)
\( \Rightarrow AB \bot \left( {SOI} \right)\,\,(*)\)
Gọi \(H\) là hình chiếu của \(O\) lên \(SI \Rightarrow OH \bot SI.\)
Từ \((*) \Rightarrow AB \bot OH \Rightarrow OH \bot (SAB) \Rightarrow OH = 12.\)Xét tam giác vuông \[SOI\] có \(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{I^2}}}\)
\( \Rightarrow \frac{1}{{O{I^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{S^2}}} = \frac{1}{{{{12}^2}}} - \frac{1}{{{{20}^2}}} = \frac{1}{{225}} \cdot \Rightarrow O{I^2} = 225 \Rightarrow OI = 15.{\rm{ }}\)
Xét tam giác vuông SOI có \(SI = \sqrt {O{S^2} + O{I^2}} = \sqrt {{{20}^2} + {{15}^2}} = 25.\)
Xét tam giác vuông OIA có \(IA = \sqrt {O{A^2} - O{I^2}} = \sqrt {{{25}^2} - {{15}^2}} = 20 \Rightarrow AB = 40.\)
Ta có \(S = {S_{ABC}} = \frac{1}{2} \cdot AB \cdot SI = \frac{1}{2} \cdot 40 \cdot 25 = 500.\)
Đáp án: 500.
Câu 43:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 44:
 Xem đáp án
Xem đáp án
Gọi \({M_0}\left( {{x_0};x_0^3 - 3x_0^2} \right)\) là tiếp điểm.
Tiếp tuyến \(\Delta \) của \((C)\) tại \({M_0}\) có dạng \(y = \left( {3x_0^2 - 6{x_0}} \right)\left( {x - {x_0}} \right) + x_0^3 - 3x_0^2\)
\(\Delta \) qua \(B\left( {0\,;\,\,b} \right)\, \Leftrightarrow b = \left( {3x_0^2 - 6{x_0}} \right)\left( {0 - {x_0}} \right) + x_0^3 - 3x_0^2 \Leftrightarrow - b = 2x_0^3 - 3x_0^2(*)\)
Có đúng một tiếp tuyến của \((C)\) đi qua điểm \(B\left( {0\,;\,\,b} \right)\, \Leftrightarrow (*)\) có đúng một nghiệm \({x_0}.\)
Đặt \[g\left( x \right) = 2{x^3} - 3{x^2}\,;\,\,g'\left( x \right) = 6{x^2} - 6x\,;\,\,g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array}} \right..\]
Ta có bảng biến thiên của hàm \(g\left( x \right)\)
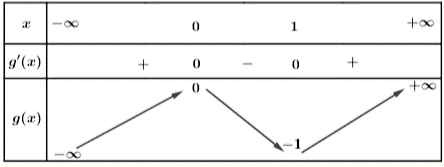
Dựa vào bảng biến thiên suy ra phương trình \((*)\) có đúng 1 nghiệm \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - b > 0}\\{ - b < - 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b < 0}\\{b > 1}\end{array}} \right.} \right..\)
Vì \(b\) nguyên và \(b \in \left( { - 10\,;\,\,10} \right)\) nên \(b \in \left\{ { - 9\,;\,\, - 8\,;\,\, \ldots \,;\,\, - 1\,;\,\,2\,;\,\,3\,;\,\, \ldots \,;\,\,9} \right\}\), suy ra 17 giá trị của \[b.\]
Đáp án: 17.
Câu 45:

 Xem đáp án
Xem đáp án
Không gian mẫu: \(n\left( \Omega \right) = 9 \cdot A_9^8\).
Lấy 4 số lẻ từ 5 số lẻ có \(C_5^4\) (cách).
Vì số 0 không ở vị trí đầu tiên và vị trí cuối cùng, mặt khác số 0 đứng giữa hai chữ số lẻ nên có 7 cách xếp vị trí số 0.
Chọn hai số lẻ trong 4 số lẻ và xếp liền kề trước và sau số 0 ta có \(A_4^2\) (cách).
Các vị trí còn lại có \(6!\) cách.
Do đó có \(7 \cdot C_5^4 \cdot A_4^2 \cdot 6!\) cách chọn số thỏa mãn đề bài.
Xác suất chọn được số thỏa mãn yêu cầu đề bài là:
\(n(A) = \frac{{7 \cdot C_5^4 \cdot A_4^2 \cdot 6!}}{{9 \cdot A_9^8}} = \frac{5}{{54}}\). Chọn D.
Câu 46:
 Xem đáp án
Xem đáp án
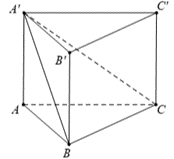
Áp dụng công thức tính nhanh sau:
Cho khối chóp \[S.ABC\]. Đặt \(SA = a\,,\,\,SB = b\,,\,\,SC = c\,,\,\,\widehat {BSC} = \alpha \,,\,\,\widehat {CSA} = \beta \,,\,\,\widehat {ASB} = \lambda .\)
Khi đó ta có: \({V_{S.ABC}} = \frac{1}{6}abc\sqrt {1 + 2\cos \alpha \cos \beta \cos \lambda - {{\cos }^2}\alpha - {{\cos }^2}\beta - {{\cos }^2}\lambda } \).
Đặt \(\widehat {AA'B} = \widehat {BA'C} = \widehat {CA'A} = \alpha = 60^\circ .\)
Ta có \({V_{A'.ABC}} = \frac{1}{6}AA' \cdot A'B \cdot A'C \cdot \sqrt {1 + 2{{\cos }^3}\alpha - 3{{\cos }^2}\alpha } = 20.\)
Suy ra thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
\[{V_{ABC.A'B'{{C'}^\prime }}} = 3{V_{A' \cdot ABC}} = 3 \cdot 20 = 60.\]
Đáp án: 60.Câu 47:
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
 Xem đáp án
Xem đáp án
Ta có đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng
\( \Leftrightarrow \) Phương trình \(2{x^2} + 6x - m - 3 = 0\) có hai nghiệm phân biệt khác 1
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{2 \cdot {1^2} + 6 \cdot 1 - m - 3 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{3^2} - 2\left( { - m - 3} \right) > 0}\\{m \ne 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - \frac{{15}}{2}}\\{m \ne 5}\end{array}} \right.} \right.} \right.\)
Vậy có 17 giá trị nguyên của \(m \in \left[ { - 10\,;\,\,10} \right]\) thỏa mãn yêu cầu đề bài.
Đáp án: 17.
Câu 48:
Cho phương trình \({\log _9}{x^2} - {\log _3}\left( {5x - 1} \right) = - {\log _3}m\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên của \(m\) để phương trình đã cho có nghiệm?
 Xem đáp án
Xem đáp án
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} > 0}\\{5x - 1 > 0}\\{m > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > \frac{1}{5}}\\{m > 0}\end{array}} \right.} \right..\)
Ta có \({\log _9}{x^2} - {\log _3}\left( {5x - 1} \right) = - {\log _3}m \Leftrightarrow {\log _{{3^2}}}{x^2} - {\log _3}\left( {5x - 1} \right) = - {\log _3}m\)
\( \Leftrightarrow {\log _3}x - {\log _3}\left( {5x - 1} \right) = {\log _3}\frac{1}{m}\)
\( \Leftrightarrow {\log _3}\frac{x}{{5x - 1}} = {\log _3}\frac{1}{m} \Leftrightarrow \frac{x}{{5x - 1}} = \frac{1}{m}\) có nghiệm
Khi và chỉ khi \(\frac{1}{m} > \frac{1}{5} \Leftrightarrow 0 < m < 5\) (dựa vào bảng biến thiên).
Mà \(m \in \mathbb{Z}\) suy ra \[m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}.\]
Đáp án: 4.
Câu 49:
Xét các số phức \[z\,,\,\,w\] thoả mãn \(\left| z \right| = 1\) và \(\left| w \right| = 2.\) Giá trị nhỏ nhất của biểu thức\(P = \left| {z + i\bar w - 6 - 8i} \right|\) là
 Xem đáp án
Xem đáp án
Ta có \(P = \left| {z + i\bar w - 6 - 8i} \right| = \left| {\left( { - 6 - 8i} \right) - \left( { - z} \right) - \left( {i \cdot \bar w} \right)} \right|\)
\( \ge \left| {\left| { - 6 - 8i} \right| - \left| { - z} \right| - \left| { - i\bar w} \right|} \right| = 10 - \left| z \right| - \left| w \right| = 10 - 1 - 2 = 7.\)
Vậy giá trị nhỏ nhất của \(P\) là 7 .
Đáp án: 7.
Câu 50:
Cho hàm số \[f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{e^x} + 1\quad {\rm{ khi }}x \ge 0}\\{{x^2} - 2x + 2\quad {\rm{ khi }}x < 0}\end{array}} \right..\] Biết \(I = \int\limits_{\frac{1}{e}}^{{e^2}} {\frac{{f(\ln x - 1)}}{x}{\rm{d}}x} = \frac{a}{b} + ce\) với \(a,\,\,b,\,\,c \in \mathbb{Z}\) và \(\frac{a}{b}\) tối giản. Tính \(a + b + c.\)
 Xem đáp án
Xem đáp án
Đặt \(t = \ln x - 1 \Rightarrow dt = \frac{{dx}}{x}.\)
Đổi cận \(x = \frac{1}{e} \Rightarrow t = - 2\) và \(x = {e^2} \Rightarrow t = 1.\)
Khi đó \(I = \int\limits_{ - 2}^1 {f\left( t \right)dt} = \int\limits_{ - 2}^1 {f\left( x \right)dx} = \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^1 {f\left( x \right)dx} \)
\( = \int\limits_{ - 2}^0 {\left( {{x^2} - 2x + 2} \right)dx} + \int\limits_0^1 {\left( {{e^x} + 1} \right)dx} \)\( = \left. {\left( {\frac{{{x^3}}}{3} - {x^2} + 2x} \right)} \right|_{ - 2}^0 + \left. {\left( {{e^x} + x} \right)} \right|_0^1 = \frac{{32}}{3} + e = \frac{a}{b} + ce{\rm{. }}\)
Suy ra \(a = 32\,,\,\,b = 3\,,\,\,c = 1.\) Vậy \(a + b + c = 36.\)
Đáp án: 36
Câu 51:
Trên tập hợp số phức, cho phương trình \({z^2} + az + b = 0\) (với \[a,\,\,b\] là số thực). Biết rằng hai số phức \(w + 1 + i\) và \(2w - 1 + 5i\) là hai nghiệm của phương trình đã cho. Tính tổng \(a + b.\)
 Xem đáp án
Xem đáp án
Ta có \({z^2} + az + b = 0\); \[w = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right){\rm{. }}\]
Phương trình (1) có 2 nghiệm phức là:
\({z_1} = w + 1 + i = x + 1 + \left( {y + 1} \right)i\); \({z_2} = 2w - 1 + 5i = 2x - 1 + \left( {2y + 5} \right)i\)
Vì \({z_1},{z_2}\) là 2 nghiệm của (1) suy ra: \({z_1} = {\bar z_2} \Rightarrow x + 1 + \left( {y + 1} \right)i = 2x - 1 - \left( {2y + 5} \right)i\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + 1 = 2x - 1}\\{y + 1 = - \left( {2y + 5} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = - 2}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{z_1} = 3 - i}\\{{z_2} = 3 + i}\end{array}} \right.} \right.} \right.\)
Theo Viète, ta có \(\left\{ {\begin{array}{*{20}{l}}{{z_1} + {z_2} = - a}\\{{z_1},{z_2} = b}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 6}\\{b = 10}\end{array} \Rightarrow a + b = 4} \right.} \right..\)
Đáp án: 4.
Câu 52:
Trong một buổi sinh hoạt nhóm của lớp 12, tổ I có 12 học sinh gồm 4 học sinh nữ trong đó có Hoa và 8 học sinh nam trong đó có Nam. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Có bao nhiêu cách chia sao cho Hoa và Nam cùng một nhóm.
 Xem đáp án
Xem đáp án
Trường hợp 1:
− Hoa và Nam cùng với 1 bạn nam và 1 bạn nữ thành một nhóm nên có duy nhất 1 cách chọn Hoa và Nam và có \(C_3^1.C_7^1\) cách chọn 1 bạn nam (trong 7 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại).
− Nhóm thứ hai có 3 bạn nam (trong 6 bạn nam còn lại) và 1 bạn nữ (trong 2 bạn nữ còn lại) nên có \(C_6^3 \cdot C_2^1\) (cách).
− Cuối cùng còn lại 3 bạn nam và 1 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.
Do đó trong trường hợp này có \(1 \cdot C_3^1 \cdot C_7^1 \cdot C_6^3 \cdot C_2^1 \cdot 1 = 840\) (cách).
Trường hợp 2:
− Hoa và Nam cùng với 2 bạn nam thành một nhóm nên có duy nhất 1 cách chọn Hoa và Nam và có \(C_7^2\) cách chọn 2 bạn nam trong 7 bạn nam còn lại.
− Nhóm thứ hai có 2 bạn nam (trong 5 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại) nên có \(C_5^2 \cdot C_3^1\) (cách).
− Cuối cùng còn lại 2 bạn nam và 2 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.
Do đó trong trường hợp này có \(1 \cdot C_7^2 \cdot C_5^2 \cdot C_3^1 \cdot 1 = 630\) (cách).
Trường hợp 3:
− Hoa và Nam cùng với 2 bạn nam thành một nhóm.
− Nhóm thứ hai có 2 bạn nam và 2 bạn nữ.
− Suy ra nhóm thứ ba có 3 bạn nam và 1 bạn nữ.
Trường hợp này trùng với trường hợp thứ hai nên ta không tính.
Suy ra có \(840 + 630 = 1\,\,470\) cách chia theo yêu cầu bài toán.
Đáp án: 1470.
Câu 53:
Trong không gian cho mặt cầu \((S):{x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right)\) thuộc đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 1 + 2t}\\{z = 2 - 3t}\end{array}} \right.\) Ba điểm \[A,\,\,B,\,\,C\] phân biệt cùng thuộc một mặt cầu sao cho \[MA,\,\,MB,\,\,MC\] là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \((ABC)\) đi qua \(D\left( {1;\,\,1;\,\,2} \right).\) Giá trị của biểu thức \(T = x_0^2 + y_0^2 + z_0^2\) bằng\[Oxyz,\]
 Xem đáp án
Xem đáp án
Mặt cầu \((S)\) có tâm \(O\left( {0\,;\,\,0\,;\,\,0} \right)\) và bán kính \[R.\]
Gọi \(M\left( {1 + {t_0}\,;\,\,1 + 2{t_0}\,;\,\,2 - 3{t_0}} \right) \in d.\)
Giả sử \(T\left( {x\,;\,\,y\,;\,\,z} \right) \in (S)\) là một tiếp điểm của tiếp tuyến \[MT\] với mặt cầu \((S).\)
Khi đó: \(O{T^2} + M{T^2} = O{M^2}\)
\( \Leftrightarrow 9 + {\left[ {x - \left( {1 + {t_0}} \right)} \right]^2} + {\left[ {y - \left( {1 + 2{t_0}} \right)} \right]^2} + {\left[ {z - \left( {2 - 3{t_0}} \right)} \right]^2} = {\left( {1 + {t_0}} \right)^2} + {\left( {1 + 2{t_0}} \right)^2} + {\left( {2 - 3{t_0}} \right)^2}\)
\( \Leftrightarrow 9 + {x^2} + {y^2} + {z^2} - 2x\left( {1 + {t_0}} \right) - 2y\left( {1 + 2{t_0}} \right) - 2z\left( {2 - 3{t_0}} \right) = 0\)
\( \Leftrightarrow \left( {1 + {t_0}} \right)x + \left( {1 + 2{t_0}} \right)y + \left( {2 - 3{t_0}} \right)z - 9 = 0.\) (vì \({x^2} + {y^2} + {z^2} = O{T^2} = 9\))
Suy ra phương trình mặt phẳng \(\left( {ABC} \right)\) có dạng: \(\left( {1 + {t_0}} \right)x + \left( {1 + 2{t_0}} \right)y + \left( {2 - 3{t_0}} \right)z - 9 = 0\)
Do \(D\left( {1\,;\,\,1\,;\,\,2} \right) \in \left( {ABC} \right)\) nên \[1 + {t_0} + 1 + 2{t_0} + 2\left( {2 - 3{t_0}} \right) - 9 = 0 \Leftrightarrow {t_0} = - 1 \Rightarrow M = \left( {0\,;\,\, - 1\,;\,\,5} \right).\]
Vậy \(T = {0^2} + {\left( { - 1} \right)^2} + {5^2} = 26.\)
Đáp án: 26.
Câu 54:
Người ta thiết kế một chiếc thùng hình trụ có thể tích \[V\] cho trước. Biết rằng chi phí làm mặt đáy và nắp của thùng bằng nhau và gấp 3 lần chi phí làm mặt xung quanh của thùng (chi phí cho một đơn vị diện tích). Gọi \[h,\,\,R\] lần lượt là chiều cao và bán kính đáy của thùng. Tỉ số \(\frac{h}{R}\) bằng bao nhiêu để chi phí sản xuất chiếc thùng là thấp nhất?
 Xem đáp án
Xem đáp án
Giả sử chi phi sản xuất mỗi đơn vị diện tích cho bề mặt xung quanh là \(a\) đồng thì chi phi sản xuất cho mỗi đơn vị diện tích của mặt đáy là \[3a\] đồng.
Chi phí sản xuất thùng là \(S = 2\pi r\ell \cdot a + 2\pi {r^2}.3a = 2\pi rh \cdot a + 2\pi \cdot {r^2} \cdot 3a\)
\( = 2a\pi r \cdot \frac{V}{{\pi {r^2}}} + 6a\pi {r^2} = \frac{{2aV}}{r} + 6a\pi {r^2} = 2a\left( {\frac{V}{r} + 3\pi {r^2}} \right) = 2a \cdot f\left( r \right)\).
Chi phí vật liệu sản xuất thùng nhỏ nhất khi \(f\left( r \right) = \frac{V}{r} + 3\pi {r^2}\) đạt giá trị nhỏ nhất.
Ta có \(f'\left( r \right) = \frac{{ - V}}{{{r^2}}} + 6\pi r = 0 \Leftrightarrow r = \sqrt[3]{{\frac{V}{{6\pi }}}}\).
Bảng biến thiên
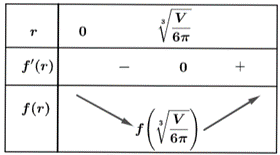
Vậy \(\min f\left( r \right) \Leftrightarrow r = \sqrt[3]{{\frac{V}{{6\pi }}}} \Rightarrow \frac{h}{r} = \frac{V}{{\pi {r^3}}} = \frac{V}{{\pi \cdot {{\left( {\sqrt[3]{{\frac{V}{{6\pi }}}}} \right)}^3}}} = 6.{\rm{ }}\)
Đáp án: 6.
Câu 55:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a,{\rm{ }}SAB\] là tam giác đều và \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right)\). Với \(\varphi \) là góc tạo bởi hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SCD} \right)\). Khi đó \(\cos \varphi \) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
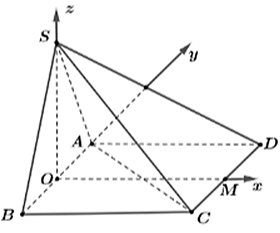
Nhận xét: Ta có thể giải bài toán với cạnh hình vuông \(a = 1.\)
Gọi \[O,\,\,M\] lần lượt là trung điểm của \[AB,\,\,CD.\]
Vì \[SAB\] là tam giác đều và \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right),\) \(SO \bot AB \Rightarrow SO \bot \left( {ABCD} \right).\)
Xét tam giác SOA vuông tại \(O\)
\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{1^2} - \frac{1}{{{2^2}}}} = \frac{{\sqrt 3 }}{2}.\)Xét hệ trục Oxyz có \(O\left( {0\,;\,\,0\,;\,\,0} \right),\,\,M\left( {1\,;\,\,0\,;\,\,0} \right),\,\,A\left( {0\,;\,\,\frac{1}{2}\,;\,\,0} \right),\,\,S\left( {0\,;\,\,0\,;\,\,\frac{{\sqrt 3 }}{2}} \right).\)
Khi đó: \(C\left( {1\,;\,\,\frac{{ - 1}}{2}\,;\,\,0} \right),\,\,D\left( {1\,;\,\,\frac{1}{2}\,;\,\,0} \right).\)
Mặt phẳng \(\left( {SAC} \right)\) có vectơ pháp tuyến \({\vec n_1} = \left[ {\overrightarrow {SC} ,\,\,\overrightarrow {AC} } \right] = \left( {\frac{{ - \sqrt 3 }}{2}\,;\,\,\frac{{ - \sqrt 3 }}{2}\,;\,\,\frac{{ - 1}}{2}} \right).\)
Mặt phẳng \(\left( {SAD} \right)\) có vectơ pháp tuyến \({\vec n_2} = \left[ {\overrightarrow {SC} ,\,\,\overrightarrow {CD} } \right] = \left( {\frac{{\sqrt 3 }}{2}\,;\,\,0\,;\,\,1} \right).\)
Vậy \(\cos \varphi = \frac{{\left| {{{\vec n}_1} \cdot {{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right| \cdot \left| {{{\vec n}_2}} \right|}} = \frac{5}{7}.\) Đáp án: \(\frac{5}{7}.\)Câu 56:
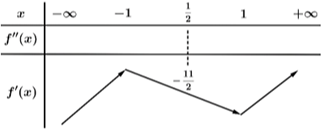
Có bao nhiêu giá trị nguyên của \(m \in \left[ { - 2020\,;\,\,2020} \right]\) để hàm số \(g\left( x \right) = {e^{ - {x^2} + \,4mx\, - \,5}} \cdot f\left( x \right)\) đồng biến trên khoảng \(\left( { - 1;\frac{1}{2}} \right)\,?\)
 Xem đáp án
Xem đáp án
Ta có: \(g'\left( x \right) = \left( { - 2x + 4m} \right){e^{ - {x^2} + \,4mx - 5}} \cdot f\left( x \right) + {e^{ - {x^2} + \,4mx - 5}} \cdot f'\left( x \right)\)
\( \Leftrightarrow g'\left( x \right) = \left[ {\left( { - 2x + 4m} \right) \cdot f\left( x \right) + f'\left( x \right)} \right] \cdot {e^{ - {x^2} + \,4mx\, - \,5}}\)
Yêu cầu bài toán \( \Leftrightarrow g'\left( x \right) \ge 0\,,\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right)\)
\( \Leftrightarrow \left( { - 2x + 4m} \right) \cdot f\left( x \right) + f'\left( x \right) \ge 0\,,\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right)\) (vì \({e^{ - {x^2} + 4mx - 5}} > 0)\)
\( \Leftrightarrow - 2x + 4m \ge - \frac{{f'\left( x \right)}}{{f\left( x \right)}},\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right)\) (vì \(f\left( x \right) > 0\,,\,\,\forall x \in \mathbb{R})\)
\( \Leftrightarrow 4m \ge 2x - \frac{{f'\left( x \right)}}{{f\left( x \right)}},\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right)\)
Xét \(h\left( x \right) = 2x - \frac{{f'\left( x \right)}}{{f\left( x \right)}},\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right).\)
Ta có \[h'\left( x \right) = 2 - \frac{{f''\left( x \right) \cdot f\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{f^2}\left( x \right)}}.\]
Mà \(\left\{ {\begin{array}{*{20}{l}}{f''\left( x \right) < 0}\\{f\left( x \right) > 0}\end{array},\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right) \Rightarrow \frac{{f''\left( x \right) \cdot f\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{f^2}\left( x \right)}} < 0,\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right)} \right.{\rm{. }}\)
Từ đó suy ra \(h'\left( x \right) > 0,\,\,\forall x \in \left( { - 1\,;\,\,\frac{1}{2}} \right).\) Vậy hàm số \(h(x)\) đồng biến trên \(\left( { - 1\,;\,\,\frac{1}{2}} \right)\)
Ta có bảng biến thiên:
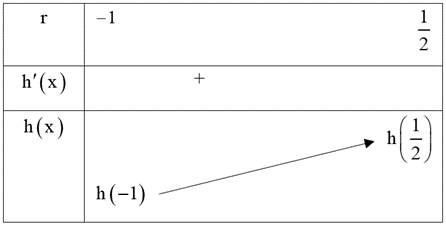
Do đó, điều kiện \((*) \Leftrightarrow 4m \ge h\left( {\frac{1}{2}} \right) \Leftrightarrow 4m \ge 2 \cdot \frac{1}{2} - \frac{{f'\left( {\frac{1}{2}} \right)}}{{f\left( {\frac{1}{2}} \right)}} \Leftrightarrow 4m \ge \frac{{225}}{{137}} \Leftrightarrow m \ge \frac{{225}}{{548}}.\)
Lại có \(\left\{ {\begin{array}{*{20}{l}}{m \in \mathbb{Z}}\\{m \in \left[ { - 2020\,;\,\,2020} \right]}\end{array} \Rightarrow m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\, \ldots \,;\,\,2020} \right\}} \right..\)
Vậy có 2020 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Đáp án: 2020.
Câu 57:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Nội dung của đoạn trích nói về văn hóa đọc sách ở Việt Nam cần được trau dồi và phát triển, nâng niu trân trọng sách giống như nâng niu, am hiểu về những chai rượu ngoại của ông tá hải quân và cách giữ gìn tủ sách như của người Do Thái. Chọn D.
Câu 58:
 Xem đáp án
Xem đáp án
Tủ sách của người Do Thái thường được để ở đầu giường để giúp trẻ được ghi nhớ hình ảnh tủ sách vào trong tiềm thức từ khi còn nhỏ, trẻ dễ nhìn, dễ thấy, dễ tiếp cận sách. Chọn D.
Câu 59:
 Xem đáp án
Xem đáp án
Tác giả mượn câu chuyện về tủ rượu ngoại của ông tá hải quân nhằm liên hệ tới việc trân trọng, giữ gìn và cần phải am hiểu về sách giống như am hiểu về rượu ngoại. Chọn B.
Câu 60:
 Xem đáp án
Xem đáp án
Tư duy trọc phú là thể hiện sự coi trọng tiền bạc hơn học thức, đề cao những giá trị về mặt vật chất hơn giá trị về tri thức. Chọn A.
Câu 61:
 Xem đáp án
Xem đáp án
Trong đoạn trích nhắc đến cách người Do Thái dạy con đọc sách ngay từ nhỏ, và thể hiện mong muốn của tác giả là mỗi người Việt Nam, mỗi gia đình Việt Nam cần tự tạo dựng thói quen đọc sách và xây dựng tủ sách. Trong đoạn trích không đề cập cụ thể việc người Việt thích khoe vật chất, không đề cao giá trị của sách. Chọn C.
Câu 62:
 Xem đáp án
Xem đáp án
Tác phẩm được viết theo thể thơ tự do. Chọn D.
Câu 63:
Thành phần biệt lập nào được sử dụng trong 2 câu thơ sau:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại.
 Xem đáp án
Xem đáp án
Hai dòng thơ đầu có sử dụng các thành phần biệt lập là: Thành phần cảm thán: “Ôi”. Thành phần tình thái: “Có ngờ đâu”. Thể hiện tâm trạng xúc động rưng rưng của nhà thơ khi trở về quê cũ. Chọn B.
Câu 64:
Xác định hai biện pháp tu từ được sử dụng trong đoạn trích sau:
Ta lại gặp những mặt người ta yêu biết mấy
Ta nhìn, ta ngắm, ta say
Ta run run nắm những bàn tay
Thương nhớ dồn trong tay ta nóng bỏng.
 Xem đáp án
Xem đáp án
Hai biện pháp tu từ được sử dụng trong đoạn trích trên là: Liệt kê và điệp từ. Từ “ta” được điệp lại nhiều lần kết hợp với một loạt những động từ “gặp”, “yêu”, “nhìn”, “say”, “ngắm”,… nhằm nhấn mạnh tình yêu quê hương tha thiết và nỗi xúc động, bồi hồi của tác giả khi trở lại quê nhà sau bao năm năm xa cách. Đồng thời tạo nhịp điệu cho câu thơ, tăng sức gợi hình gợi cảm cho sự diễn đạt. Chọn C.
Câu 65:
Biện pháp tu từ nào được sử dụng trong đoạn thơ dưới đây?
Ơi những bông trang trắng, những bông trang hồng
Như tấm lòng em trong trắng thủy chung
Như trái tim em đẹp màu đỏ thắm
 Xem đáp án
Xem đáp án
So sánh: Những bông trang trắng, những bông trang hồng – tấm lòng em, trái tim em. Chọn A.
Câu 66:
 Xem đáp án
Xem đáp án
Những hình ảnh trong đoạn trích đã thể hiện được vẻ đẹp và sức sống tiềm tàng, mãnh liệt của quê hương là: xanh biếc bóng dừa, những mặt người ta yêu biết mấy, đoạn đường xưa, tiếng võng đưa, những bông trang trắng, những bông trang hồng, con sông nước chẳng đổi dòng, hoa lục bình tím cả bờ sông. Chọn D.
Câu 67:
 Xem đáp án
Xem đáp án
Ở đoạn trích trên các phương án A, B, C đều chưa đầy đủ, chưa bao quát hết được toàn bộ nội dung của đoạn trích bởi chỉ đề cập đến một khía cạnh nội dung mà đoạn trích nói đến. Chọn D.
Câu 68:
 Xem đáp án
Xem đáp án
Dựa vào các chi tiết: Thục Phán đắp lũy thành Cổ Loa cũng là đắp đê phòng lụt. Sử biên niên nhà Hán chép rằng, ở đầu công nguyên, huyện Phong Khê (Đông Anh) đã có đê phòng lụt. Đê sẽ làm cho quá trình bồi tụ tự nhiên bị ngăn chặn lại, ít nhất là từng phần. Cho nên đất Hà Nội nội thành, bên hồ Tây và dòng Tô Lịch, lại có rất nhiều đầm hồ. → Nội thành Hà Nội có nhiều đầm hồ là do ảnh hưởng của quá trình đắp đê phòng lụt từ xa xưa. Chọn C.
Câu 69:
 Xem đáp án
Xem đáp án
Đây là câu hỏi suy luận. Cần chú ý đến mục đích vốn có của việc đắp lũy Cổ Loa là để chống giặc (mục đích này không được nhắc đến trực tiếp trong đoạn trích) nhưng có thể suy ra từ đoạn trích. Khi tác giả dùng từ “cũng” trong câu: “Thục Phán đắp lũy thành Cổ Loa cũng là đắp đê phòng lụt” thì có nghĩa việc phòng lụt chỉ là mục đích đi kèm, mục đích phụ của việc đắp thành lũy Cổ Loa. Chọn B.
Câu 70:
 Xem đáp án
Xem đáp án
- Phương án A, B: Thông tin có trong câu: Sông hồ không những là nguồn nước dùng trong sinh hoạt mà còn là hệ thống thuỷ lợi và giao thông truyền thống.
- Phương án C: Thông tin có trong câu: Sông hồ cũng là những sự kiện địa lí được dùng làm nguyên lí sơ khởi chỉ đạo việc quy tụ xóm làng, phường và thành lũy phòng vệ (sử dụng những đoạn sông Hồng, sông Tô làm ngoại hào).
- Phương án D: Thông tin không được nhắc đến trong đoạn trích.
→ Chọn D.
Câu 71:
 Xem đáp án
Xem đáp án
Từ “du đãng” xuất hiện trong câu văn: Có đời sống du đãng tự nhiên của những con sông ở đồng bằng do chính chúng tạo thành.... Ta có thể bám vào cụm từ “do chính chúng tạo thành” tức là không bị phụ thuộc vào ai, không bị yếu tố nào khác tác động để xác định từ “du đãng” trong đoạn trích gần nghĩa nhất với từ “tự do”. Chọn D.
Câu 72:
 Xem đáp án
Xem đáp án
Đoạn trích được viết theo phương thức biểu đạt là: biểu cảm. Chọn A.
Câu 73:
 Xem đáp án
Xem đáp án
Câu 74:
 Xem đáp án
Xem đáp án
Ý nghĩa của câu thơ: Biết khao khát những điều anh mơ ước: xuất phát từ tình yêu và sự tôn trọng đối với người mình yêu, nhân vật “em” đồng cảm và sống hết mình với ước mơ của người mình yêu. Chọn C.
Câu 75:
 Xem đáp án
Xem đáp án
Những từ nêu lên những trạng thái cảm xúc, tình cảm của nhân vật “em”: khao khát, xúc động, yêu. Chọn B.
Câu 76:
 Xem đáp án
Xem đáp án
Các đáp án A, B, C đều là những thông điệp được gửi gắm trong đoạn thơ. Chỉ có đáp án D không phải là thông điệp nhà thơ muốn gửi gắm. Chọn D.
Câu 77:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Nhà báo cần phải thường xuyên xâm nhập đời sống thực tế của xã hội để viết bài.
 Xem đáp án
Xem đáp án
“xâm nhập” có nghĩa là đi vào một cách trái phép, thường gây ra tác hại; từ đúng trong câu này là “thâm nhập”: đi sâu vào và cùng hoà mình trong một môi trường hoạt động nào đó. Chọn B.
Câu 78:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Truyện ngắn Những đứa con trong gia đình giống như giọt nước mang hình cả bầu trời của dân tộc ta, của người dân Bắc Bộ trong một hành trình đánh giặc lâu dài, bền bỉ, kiên cường.
 Xem đáp án
Xem đáp án
Truyện ngắn Những đứa con trong gia đình giống như giọt nước mang hình cả bầu trời của dân tộc ta, của người dân Nam Bộ trong một hành trình đánh giặc lâu dài, bền bỉ, kiên cường. Chọn B.
Câu 79:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Vợ chồng A Phủ là câu chuyện về những người dân lao động vùng cao Tây Bắc không cam chịu bọn thực dân, chúa đất áp bức, đày đọa, giam hãm trong cuộc sống tăm tối đã vùng lên phản kháng, tìm cuộc sống bình thường.
 Xem đáp án
Xem đáp án
Nội dung câu văn là thể hiện quá trình đấu tranh của người dân vùng cao Tây Bắc chống lại bọn thực dân, chúa đất đã giam hãm để có cuộc sống tự do. Cụm từ “cuộc sống bình thường” sử dụng chưa phù hợp. Chọn D.
Câu 80:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Lục bát được coi là niềm kiêu hãnh của thơ Việt bởi phần hồn của dân ta đã vay mượn ở đó nhiều nhất, sâu nhất. Có thể nói, người Việt sống trong bầu thi quyển lục bát.
 Xem đáp án
Xem đáp án
Đoạn văn trên thể hiện niềm tự hào của người Việt đối với thể thơ lục bát. Thơ lục bát mang đặc trưng của người Việt, thể hiện tới đời sống tinh thần của nhân dân. Từ “vay mượn” ở đây là từ sai ngữ nghĩa vì thơ ca là sản phẩm của con người tức là con người có trước rồi mới có thơ ca nên phần hồn của con người không thể “vay mượn” từ thơ ca được. Thay “vay mượn” bằng “nương náu”. Chọn C.
Câu 81:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Hai mươi năm đã trôi qua kể từ ngày sau khi bố tôi mất, tôi chưa có dịp trở lại quê nhà.
 Xem đáp án
Xem đáp án
Cụm từ “sau khi” là thừa trong câu này; sự có mặt của nó trong câu làm cho ý diễn đạt bị rối, không rõ nghĩa. Chọn C.
Câu 82:
 Xem đáp án
Xem đáp án
Từ “mắt bồ câu” là đôi mắt to tròn, đẹp và trong sáng như mắt chim bồ câu (mắt được dùng với nghĩa đen); các từ còn lại trong nhóm (mắt lưới, mắt bão, mắt na) đều được dùng với nghĩa chuyển. Chọn C.
Câu 83:
 Xem đáp án
Xem đáp án
Các từ “nhấp nhô, cuồn cuộn, lăn tăn” là các từ đồng nghĩa dùng để chỉ trạng thái vận động của con sóng. Từ “nhấp nhổm” là từ dùng để chỉ hoạt động trạng thái của con người. Chọn D.
Câu 84:
 Xem đáp án
Xem đáp án
Các từ “ăn, nhai, cắn” là các từ chỉ hoạt động của răng miệng. “Nhìn” là từ chỉ hoạt động của mắt. Chọn C.
Câu 85:
 Xem đáp án
Xem đáp án
Nền văn học có tính chất hướng nội, quan tâm nhiều hơn tới số phận cá nhân không phải là đặc điểm của văn học Việt Nam giai đoạn 1945 – 1975. Đây là đặc điểm của văn học sau năm 1975. Chọn C.
Câu 86:
 Xem đáp án
Xem đáp án
Các từ “đo đỏ, tim tím, xanh xanh” chỉ màu sắc; “thăm thẳm” chỉ độ sâu. Chọn D.
Câu 87:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tiếng Việt thuộc họ ngôn ngữ _________, dòng Môn - Khmer và có quan hệ gần gũi với tiếng Mường.
 Xem đáp án
Xem đáp án
Tiếng Việt thuộc họ ngôn ngữ Nam Á, dòng Môn - Khmer và có quan hệ gần gũi với tiếng Mường. Chọn A.
Câu 88:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Hai mẹ con Cám hí hửng sắm sửa quần lành, áo tốt, _______ Tấm _______ quần áo rách mướp.
 Xem đáp án
Xem đáp án
Hai mẹ con Cám hí hửng sắm sửa quần lành, áo tốt, còn Tấm vẫn quần áo rách mướp. Chọn B.
Câu 89:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Ca dao là tác phẩm thơ _________, thường kết hợp với âm nhạc khi diễn xướng, được sáng tác nhằm diễn tả thế giới nội tâm của con người.
 Xem đáp án
Xem đáp án
Ca dao là tác phẩm thơ trữ tình dân gian, thường kết hợp với âm nhạc khi diễn xướng, được
Ca dao là tác phẩm thơ trữ tình dân gian, thường kết hợp với âm nhạc khi diễn xướng, được sáng tác nhằm diễn tả thế giới nội tâm của con người. Chọn D.
sáng tác nhằm diễn tả thế giới nội tâm của con người. Chọn D.
Câu 90:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Nghệ thuật lập luận của Hồ Chí Minh thể hiện một trình độ tư duy sắc sảo, một tầm nhìn bao quát và một trái tim luôn hướng về công lí, _______, chính nghĩa.
 Xem đáp án
Xem đáp án
Nghệ thuật lập luận của Hồ Chí Minh thể hiện một trình độ tư duy sắc sảo, một tầm nhìn bao quát và một trái tim luôn hướng về công lí, lẽ phải, chính nghĩa. Chọn C.
Câu 91:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Văn học Việt Nam từ năm 1945 đến năm 1975 đã _________ và _________ mạnh mẽ những yếu tố truyền thống tư tưởng lớn của dân tộc: chủ nghĩa nhân đạo, đặc biệt là chủ nghĩa yêu nước và chủ nghĩa anh hùng.
 Xem đáp án
Xem đáp án
Những yếu tố truyền thống từ tư tưởng dân tộc: chủ nghĩa nhân đạo, chủ nghĩa yêu nước và chủ nghĩa anh hùng đều là những truyền thống tốt đẹp của dân tộc thường được đề cập tới trong văn học dân gian và văn học trung đại, vì thế văn học giai đoạn 1945 – 1975 “kế thừa” (tiếp nhận những thứ tốt đẹp của cha ông để lại) và “phát huy” (làm nó tốt lên, nhiều lên). Chọn A.
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Còn xa lắm mới đến cái thác dưới. Nhưng đã thấy tiếng nước réo gần mãi lại réo to mãi lên. Tiếng nước thác nghe như là oán trách gì, rồi lại như là van xin, rồi lại như là khiêu khích, giọng gằn mà chế nhạo. Thế rồi nó rống lên như tiếng một ngàn con trâu mộng đang lồng lộn giữa rừng vầu rừng tre nứa nổ lửa, đang phá tuông rừng lửa, rừng lửa cùng gầm thét với đàn trâu da cháy bùng bùng.
(Người lái đò Sông Đà – Nguyễn Tuân)
Đoạn trích trên thể hiện thái độ gì của tác giả đối với vẻ đẹp hùng vĩ của con sông Đà?
 Xem đáp án
Xem đáp án
Được chứng kiến tận mắt sự dữ dội, hùng vĩ của con sông Đà, với những so sánh liên tưởng thú vị “tiếng nước thác nghe như là oán trách gì, rồi lại như là van xin, rồi lại như là khiêu khích, giọng gằn mà chế nhạo....” có thể thấy thái độ của tác giả rất say mê, hứng khởi. Chọn B.
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Buổi ấy, bao nhiêu những loài trân cầm dị thú, cổ mộc quái thạch, chậu hoa cây cảnh ở chốn nhân gian, Chúa đều ra sức thu lấy, không thiếu một thứ gì. Có khi lấy cả cây đa to, cành lá rườm rà, từ bên bắc chở qua sông đem về. Nó giống như một cây cổ thụ mọc trên đầu non hốc đá, rễ dài ra đến vài trượng, phải một cơ binh khiêng mới nổi, lại bốn người đi kèm, đều cầm gươm, đánh thanh la đốc thúc quân lính khiêng đi cho đều tay. Trong phủ, tùy chỗ điểm xuyết bày vẽ ra hình núi non bộ trông như bến bể đầu non. Mỗi khi đêm thanh vắng, tiếng chim kêu vượn hót ran khắp bốn bề, hoặc nửa đêm ồn ào như trận mưa sa gió táp, vỡ tổ tan đàn, kẻ thức giả biết đó là triệu bất thường.
(Phạm Đình Hổ, Chuyện cũ trong phủ Chúa Trịnh, Ngữ văn 9, tập hai,
NXB Giáo dục Việt Nam, 2019)
Cách kể trong đoạn trích có tác dụng gì?
 Xem đáp án
Xem đáp án
Xác định các chi tiết có trong đoạn trích:
- “Chúa đều ra sức thu lấy, không thiếu một thứ gì”: Chúa Trịnh dùng quyền lực để cướp bóc những thứ của quý trong thiên hạ về tô điểm cho phủ Chúa.
- “phải một cơ binh khiêng mới nổi, lại bốn người đi kèm, đều cầm gươm, đánh thanh la đốc thúc quân lính khiêng đi cho đều tay”: Sự phô trương, hao tốn sức người vào những việc không đáng.
- “Mỗi khi đêm thanh vắng, tiếng chim kêu vượn hót ran khắp bốn bề, hoặc nửa đêm ồn ào như trận mưa sa gió táp, vỡ tổ tan đàn, kẻ thức giả biết đó là triệu bất thường”: dự báo về sự sụp đổ của Chúa Trịnh.
→ Đoạn trích kể lại câu chuyện Chúa Trịnh sử dụng quyền lực để vơ vét, cướp bóc của quý trong thiên hạ. Giọng điệu phê phán, chê trách, không đồng tình. Chọn A.
Câu 94:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Anh bạn dãi dầu không bước nữa,
Gục lên súng mũ bỏ quên đời!
Chiều chiều oai linh thác gầm thét,
Đêm đêm Mường Hịch cọp trêu người.
(Tây Tiến – Quang Dũng)
Cụm từ “bỏ quên đời” được in đậm trong đoạn trích thể hiện ý nghĩa gì?
 Xem đáp án
Xem đáp án
Cụm từ “bỏ quên đời” là cách nói giảm nói tránh về cái chết, gợi tư thế ngạo nghễ không chút bi lụy của người lính Tây Tiến. Chọn A.
Câu 95:
Đọc đoạn trích sau và trả lời câu hỏi:
Từ ấy trong tôi bừng nắng hạ
Mặt trời chân lí chói qua tim
Hồn tôi là một vườn hoa lá
Rất đậm hương và rộn tiếng chim...
(Trích Từ ấy – Tố Hữu)
Biện pháp tu từ nào được sử dụng trong hai câu thơ in đậm?
 Xem đáp án
Xem đáp án
Ẩn dụ: nắng hạ, mặt trời chân lí → chỉ lí tưởng cách mạng, ánh sáng của Đảng. Chọn C.
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Vũ trụ nội mạc phi phận sự,
Ông Hi Văn tài bộ đã vào lồng.
Khi Thủ khoa, khi Tham tán, khi Tổng đốc Đông,
Gồm thao lược đã nên tay ngất ngưởng.
Lúc bình Tây, cờ đại tướng,
Có khi về Phủ doãn Thừa Thiên.
(Bài ca ngất ngưởng – Nguyễn Công Trứ)
Biện pháp tu từ nào được sử dụng đế nhắc đến những chức vụ, địa vị mà ông Hi Văn đã kinh qua?
 Xem đáp án
Xem đáp án
Liệt kê: Khi Thủ khoa, khi Tham tán, khi Tổng đốc Đông,… Chọn D.
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trong hoàn cảnh đề lao, người ta sống bằng tàn nhẫn, bằng lừa lọc, tính cách dịu dàng và lòng biết giá người, biết trọng người ngay của viên quan coi ngục này là một thanh âm trong trẻo chen vào giữa một bản đàn mà nhạc luật đều hỗn loạn xô bồ.
Ông trời nhiều khi chơi ác, đem đày ải những cái thuần khiết vào giữa một đống cặn bã. Và những người có tâm điền (lòng dạ con người) tốt và thẳng thắn, lại phải ăn đời ở kiếp với lũ quay quắt.
Ngục quan lấy làm nghĩ ngợi về câu nói ban chiều của thầy thơ lại: “Có lẽ lão bát này, cũng là một người khá đây. Có lẽ, hắn cũng như mình, chọn nhầm nghề mất rồi. Một kẻ biết kính mến khí phách, một kẻ biết tiếc, biết trọng người có tài, hẳn không phải là kẻ xấu hay là vô tình. Ta muốn biệt đãi ông Huấn Cao, ta muốn cho ông ta đỡ cực trong những ngày cuối cùng còn lại, nhưng chỉ sợ tên bát phẩm thơ lại này đem cáo giác với quan trên thì khó mà ở yên. Để mai ta dò ý tứ hắn lần nữa xem sao rồi sẽ liệu…
(Chữ người tử tù – Nguyễn Tuân)
Nét nổi bật nhất về nghệ thuật của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Đoạn trích trong tác phẩm “Chữ người tử tù” của Nguyễn Tuân trong hoàn cảnh đêm trước khi quản ngục nhận Huấn Cao về buồng giam. Đây là lúc ông đang suy ngẫm về ý nghĩa của cuộc đời và cái đẹp trong cuộc đời mình. Chọn D.
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Dữ dội và dịu êm
Ồn ào và lặng lẽ
Sông không hiểu nổi mình
Sóng tìm ra tận bể.
(Trích Sóng – Xuân Quỳnh)
Dòng nào dưới đây chứa những biện pháp tu từ xuất hiện trong đoạn thơ?
 Xem đáp án
Xem đáp án
Các biện pháp tu từ xuất hiện trong đoạn thơ trên là: liệt kê, ẩn dụ, nhân hóa, đối lập.
+ Liệt kê các trạng thái của sóng (dữ dội, dịu êm, ồn ào, lặng lẽ).
+ Ẩn dụ hình ảnh “sông” và “sóng” cho chủ thể trữ tình cô gái và chàng trai.
+ Nhân hóa “sông không hiểu mình” và “sóng tìm ra tận bể”.
+ Đối lập: khắc họa các trạng thái đối lập của sóng (dữ dội >< dịu êm; ồn ào >< lặng lẽ).
→ Chọn D.
Câu 99:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Chợ họp giữa phố vãn từ lâu. Người về hết và tiếng ồn ào cũng mất. Trên đất chỉ còn rác rưởi, vỏ bưởi, vỏ thị, lá nhãn và lá mía. Một mùi âm ẩm bốc lên, hơi nóng của ban ngày lẫn với mùi cát bụi quen thuộc quá, khiến chị em Liên tưởng là mùi riêng của đất, của quê hương này.
(Hai đứa trẻ – Thạch Lam)
Chi tiết in đậm trong đoạn văn khắc hoạ đặc điểm nào trong tâm hồn nhân vật Liên?
 Xem đáp án
Xem đáp án
Chi tiết “Một mùi âm ẩm bốc lên, hơi nóng của ban ngày lẫn với mùi cát bụi quen thuộc quá, khiến chị em Liên tưởng là mùi riêng của đất, của quê hương này” thể hiện tâm hồn nhạy cảm của nhân vật Liên. Chọn B.
Câu 100:
Đọc đoạn trích sau và trả lời câu hỏi:
Chiều chiều oai linh thác gầm thét
Đêm đêm Mường Hịch cọp trêu người.
(Tây Tiến – Quang Dũng)
Nội dung chính của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Nội dung chính trong đoạn thơ là: Gợi tả sự dữ dội, hoang sơ, bí hiểm và đầy đe dọa của núi rừng miền Tây. Chọn A.
Câu 101:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thị cắp cái thúng con, đầu hơi cúi, cái nón rách tàng nghiêng nghiêng che khuất đi nửa mặt. Thị có vẻ rón rén, e thẹn. Mấy đứa trẻ con thấy lạ vội chạy ra đón xem. Sợ chúng nó đùa như ngày trước, Tràng vội vàng nghiêm nét mặt, lắc đầu ra hiệu không bằng lòng.
(Vợ nhặt – Kim Lân)
Tình cảm, thái độ nào của anh cu Tràng được khắc họa qua đoạn văn trên?
 Xem đáp án
Xem đáp án
Những câu văn trên khắc họa thái độ sợ người đàn bà xấu hổ khi bị đám trẻ trêu và tôn trọng người đàn bà của Tràng. Chọn D.
Câu 102:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Ngô Tử Văn tên là Soạn, người làng Yên Dũng, đất Lạng Giang. Chàng vốn khảng khái, nóng nảy, thấy sự tà gian thì không thể chịu được, vùng Bắc người ta vẫn khen là người cương trực. Trong làng trước có một ngôi đền linh ứng lắm. Cuối đời nhà Hồ, quân Ngô sang lấn cướp, vùng ấy thành một nơi chiến trường. Bộ tướng của Mộc Thạnh có viên Bách hộ họ Thôi, tử trận ở gần đền, từ đấy làm yêu quái trong dân gian. Tử Văn rất tức giận, một hôm tắm gội sạch sẽ, khấn trời, rồi châm lửa đốt đền. Mọi người đều lắc đầu lè lưỡi, lo sợ thay cho Tử Văn, nhưng chàng vẫn vung tay không cần gì cả.
(Chuyện chức phán sự đền Tản Viên – Nguyễn Dữ)
Xác định phương thức biểu đạt chính trong đoạn trích trên.
 Xem đáp án
Xem đáp án
Nội dung văn bản là chuỗi sự việc:
+ Giới thiệu về Ngô Tử Văn (tên, quê quán, tính tình).
+ Sự việc quân Ngô sang xâm lược nước ta.
+ Sự việc viên tướng của Mộc Thạnh tử trận và làm yêu quái.
+ Sự kiện Ngô Tử Văn đi đốt đền.
Các yếu tố miêu tả về Tử Văn (tính khảng khái, nóng nảy...) có xuất hiện nhưng không phải phương thức biểu đạt chính của đoạn trích. Yếu tố biểu cảm, thuyết minh không có trong văn bản trên. Chọn A.
Câu 103:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thuyền tôi trôi trên Sông Đà. Cảnh ven sông ở đây lặng tờ. Hình như từ đời Lí, đời Trần, đời Lê, quãng sông này cũng lặng tờ đến thế mà thôi. Thuyền tôi trôi qua một nương ngô nhú lên mấy lá ngô non đầu mùa. Mà tịnh không một bóng người, cỏ gianh và đồi núi đang ra những nõn búp. Một đàn hươu cúi đầu ngốn búp cỏ gianh đẫm sương đêm. Bờ sông hoang dại như một bờ tiền sử. Bờ sông hồn nhiên như một nỗi niềm cổ tích tuổi xưa. Chao ôi, thấy thèm được giật mình vì một tiếng còi xúp-lê của một chuyến xe lửa đầu tiên đường sắt Phú Thọ - Yên Bái - Lai Châu. Con hươu thơ ngộ ngẩng đầu nhung khỏi áng cỏ sương, chăm chăm nhìn tôi không chớp mắt mà như hỏi tôi bằng cái tiếng nói riêng của con vật lành: “Hỡi ông khách Sông Đà, có phải ông vừa nghe thấy một tiếng còi sương?”. Đàn cá dầm xanh quẫy vọt lên mặt sông bụng trắng như bạc rơi thoi. Tiếng cá đập nước sông đuổi mất đàn hươu vụt biến. Thuyền tôi trôi trên “Dải Sông Đà bọt nước lênh đênh - Bao nhiêu cảnh bấy nhiêu tình” của “một người tình nhân chưa quen biết” (Tản Đà). Dòng sông quãng này lững lờ như nhớ thương những hòn đá thác xa xôi để lại trên thượng nguồn Tây Bắc.
(Người lái đò Sông Đà – Nguyễn Tuân)
Nội dung chính của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Đoạn trích miêu tả vẻ đẹp trữ tình của dòng sông Đà. Chọn B.
Câu 104:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thêm một tuổi đời, vậy là cái tuổi ba mươi đâu còn xa nữa. Vài năm nữa thôi mình sẽ trở thành một chị cán bộ già dặn đứng đắn. Nghĩ đến đó mình thoáng thấy buồn. Tuổi xuân của mình đã qua đi trong lửa khói, chiến tranh đã cướp mất hạnh phúc trong tình yêu và tuổi trẻ. Ai lại không tha thiết với mùa xuân, ai lại không muốn cái sáng ngời trong đôi mắt và trên đôi môi căng mọng khi cuộc đời còn ở tuổi hai mươi? Nhưng… tuổi hai mươi của thời đại này đã phải dẹp lại những ước mơ hạnh phúc mà lẽ ra họ phải có…
(Nhật kí Đặng Thùy Trâm – NXB Hội Nhà Văn, 2005)
Biện pháp tu từ nào được sử dụng trong câu văn in đậm ở đoạn trích trên?
 Xem đáp án
Xem đáp án
Điệp ngữ “ai lại không”. Câu hỏi tu từ: “Ai lại không tha thiết với mùa xuân, ai lại không muốn cái sáng ngời trong đôi mắt và trên đôi môi căng mọng khi cuộc đời còn ở tuổi hai mươi?”. Chọn A.
Câu 105:
Đọc đoạn trích sau và trả lời câu hỏi:
Quanh năm buôn bán ở mom sông,
Nuôi đủ năm con với một chồng.
Lặn lội thân cò khi quãng vắng,
Eo sèo mặt nước buổi đò đông.
Một duyên hai nợ âu đành phận,
Năm nắng mười mưa dám quản công.
(Thương vợ – Trần Tế Xương)
Trần Tế Xương mượn hình ảnh con cò trong ca dao để nói lên điều gì?
 Xem đáp án
Xem đáp án
Thấm thía nỗi vất vả, gian lao của vợ, Tú Xương đã mượn hình ảnh con cò trong ca dao để nói về bà Tú: thân cò lầm lũi gợi liên tưởng về thân phận vất vả, khổ cực của bà Tú cũng như những người phụ nữ Việt Nam trong xã hội xưa. Chọn D.
Câu 106:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Em nghĩ về anh, em
Em nghĩ về biển lớn
Từ nơi nào sóng lên?
Sóng bắt đầu từ gió
Gió bắt đầu từ đâu?
(Sóng – Xuân Quỳnh)
Ý chính của đoạn thơ là gì?
 Xem đáp án
Xem đáp án
Đoạn thơ thể hiện niềm suy tư, trăn trở của người phụ nữ trong tình yêu. Chọn C.
Câu 107:
 Xem đáp án
Xem đáp án
Ấn Độ là thuộc địa của thực dân Anh. Sau Chiến tranh thế giới thứ hai cuộc đấu tranh chống thực dân Anh, đòi độc lập của nhân dân Ấn Độ phát triển mạnh mẽ. Trước sức ép của phong trào, thực dân Anh phải nhượng bộ, trao quyền tự trị cho Án Độ. Theo kế hoạch Maobáttơn, Án Độ được chia thành 2 nước: Ấn Độ (theo Ấn Độ giáo), Pakistan (Hồi giáo). Không chấp nhận quy chế tự trị, Đảng Quốc Đại lãnh đạo nhân dân Án Độ tiếp tục đấu tranh đòi độc lập. Ngày 26-01-1950, Ấn Độ tuyên bố độc lập và thành lập nước Cộng hòa. Chọn B.
Câu 108:
 Xem đáp án
Xem đáp án
Phong trào Cần Vương và phong trào Yên Thế cuối thế kỉ XIX nổ ra chịu sự chi phối của hệ tư tưởng phong kiến với quan điểm trung quân, ái quốc, giành độc lập, lập lại quốc gia phong kiến độc lập. Chọn A.
Câu 109:
 Xem đáp án
Xem đáp án
Lực lượng xã hội đông đảo nhất ở Việt Nam trong cuộc khai thác thuộc địa lần thứ hai của thực dân Pháp (1919 1929) là nông dân, chiếm hơn 90% dân số cả nước. Chọn A.
Câu 110:
 Xem đáp án
Xem đáp án
Đến những năm 70 của thế kỉ XX, phong trào giải phóng dân tộc trên thế giới đã phát triển mạnh ở cả châu Á, Phi và khu vực Mĩ latinh, nhiều quốc gia độc lập đã ra đời. Đây chính là một trong những nguyên dẫn đến sự xuất hiện của xu thế hòa hoãn Đông-Tây. Sau khi xu thế hòa hoãn Đông-Tây xuất hiện thì những vấn đề giữa 2 nước Đức mới từng bước được giải quyết. Phương án C và D không có tác động hay ảnh hướng dân tới xu thế hòa hoãn Đông-Tây trong những năm 70 của thế kỉ XX. Chọn A.
Câu 111:
 Xem đáp án
Xem đáp án
Năm 1919, Nguyễn Ái Quốc gửi đến Hội nghị Vécxai Bản yêu sách của nhân dân An Nam đòi Chính phủ Pháp thừa nhận quyền tự do, dân chủ, quyền bình đẳng và quyền tự quyết của dân tộc Việt Nam. Chọn A.
Câu 112:
 Xem đáp án
Xem đáp án
Việt Nam trong thời kì 1954-1975 chỉ có miền Bắc tiến lên chủ nghĩa xã hội còn miền Nam vẫn đấu tranh chống Mĩ cứu nước nên phương án D sai, Chọn D.
Câu 113:
 Xem đáp án
Xem đáp án
Hội nghị thành lập Đảng Cộng sản Việt Nam (đầu năm 1930) được đánh giá là mang tầm vóc của một đại hội thành lập Đảng, vi đã hợp nhất các tổ chức cộng sản thành một đảng cộng sản duy nhất, thông qua Cương lĩnh chính trị đầu tiên của Đảng. Cương lĩnh chính trị là một cương lĩnh cách mạng giải phóng dân tộc sáng tạo, kết hợp đúng đến vấn đề dân tộc và vấn đề giai cấp. Độc lập và tự do là tư tưởng cốt lỡi của cương lĩnh này. Chọn B.
Câu 114:
 Xem đáp án
Xem đáp án
Khi địch vừa tiến công Việt Bắc, Đảng ta đã có chỉ thị "Phải phá tan cuộc tiến công mùa đông của giặc Pháp". Chọn C.
Câu 115:
 Xem đáp án
Xem đáp án
Ở thời điểm cuối năm 1947, thực dân Pháp vẫn nắm giữ thế chủ động trên chiến trường chính (Bắc Bộ). Chọn A.
Câu 116:
 Xem đáp án
Xem đáp án
Trong chiến dịch Việt Bắc thu-đông năm 1947, cách đánh du kích được bộ đội Việt Nam sử dụng phổ biến. Chọn D.
Câu 117:
 Xem đáp án
Xem đáp án
Khu vực Đông Nam Á tiếp giáp hai đại dương là Thái Bình Dương và Án Độ Dương. Chọn B.
Câu 118:
 Xem đáp án
Xem đáp án
Tỉ lệ người già trong dân số ngày càng cao không phải thuận lợi cho phát triển kinh tế-xã hội. Chọn B.
Câu 119:
 Xem đáp án
Xem đáp án
Vùng nước nằm trong đường nước cơ sở được gọi là vùng nội thủy. Chọn B.
Câu 120:
 Xem đáp án
Xem đáp án
Tây Nguyên có sự đối lập với đồng bằng ven biển miền Trung về mùa mưa và mủa khô do ảnh hưởng của địa hình và gió. Chọn A.
Câu 121:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- A sai: dân tộc Bana, Xơ-đăng, Chăm chủ yếu ở Tây Nguyên
- B sai: dân tộc Tày, Thái, Nùng, Giáy, Lào tập trung ở miền núi phía Bắc
- C sai: dân tộc Kinh tập trung đông đúc ở vùng đồng bằng và ven biển
- D đúng: các dân tộc ít người phân bố tập trung chủ yếu ở miền núi. Chọn D.
Câu 122:
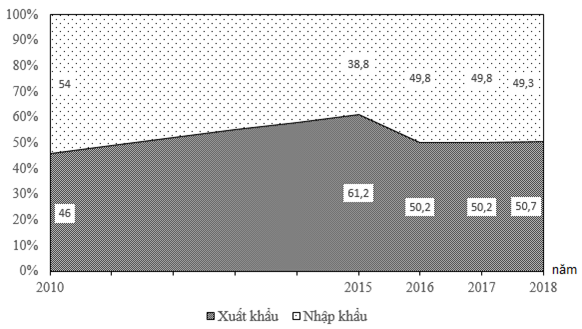
(Nguồn: Niên giám thống kê Việt Nam 2018, NXB Thống kê, 2019)
Biểu đồ thể hiện nội dung nào sau đây?
 Xem đáp án
Xem đáp án
Biểu đồ miền → thể hiện sự chuyển dịch cơ cấu → Biểu đồ đã cho thể hiện sự chuyển dịch cơ cấu giá trị xuất nhập khẩu của nước ta giai đọa 2010-2018. Chọn B.
Câu 123:
 Xem đáp án
Xem đáp án
Ngành chăn nuôi điều kiện quan trọng nhất là cần có cơ sở thức ăn đảm bảo. Với các nước đang phát triển chưa đáp ứng được điều này → Chọn B.
Câu 124:
 Xem đáp án
Xem đáp án
Di tích, lễ hội là tài nguyên nhân văn → loại → Chọn D.
Câu 125:
 Xem đáp án
Xem đáp án
Nhân tố tự nhiên được coi là quan trọng nhất để vùng Tây Nguyên phát triển cây cà phê là đất và khí hậu → Chọn D.
Câu 126:
 Xem đáp án
Xem đáp án
Vai trò quan trọng nhất của công trình thủy lợi hồ Dầu Tiếng ở Đông Nam Bộ là cung cấp nước tưới cho các vùng chuyên canh. Thủy lợi → cung cấp nước tưới. Chọn C.
Câu 127:
 Xem đáp án
Xem đáp án
Tia gamma có bản chất là sóng điện từ, không mang điện nên không bị lệch trong điện trường và từ trường.
Tia \(\alpha \) là dòng hạt nhân nguyên tử \(_2^4He\) mang điện tích \( + 2e\), có xu hướng bị lệch về phía bản âm của tụ điện.
Tia \({\beta ^ + }\) có bản chất là dòng hạt poziton mang điện tích \( + 1e\), có xu hướng bị lệch về phía bản âm của tụ điện.
Tia \({\beta ^ - }\) có bản chất là dòng hạt electron mang điện tích \( - 1e\), có xu hướng lệch về phía bản dương của tụ điện.
Chọn A.
Câu 128:
 Xem đáp án
Xem đáp án
Khoảng cách giữa hai vân sáng liền kề là:
\(i = \frac{{\lambda D}}{a} \Rightarrow \lambda = \frac{{ai}}{D} = \frac{{0,{{1.10}^{ - 3}}{{.8.10}^{ - 3}}}}{2} = {4.10^{ - 7}}{\mkern 1mu} {\mkern 1mu} \left( m \right)\).
Hiệu đường đi của tia sáng từ hai khe tới vân tối thứ 2 kể từ vân trung tâm (k = 1) là:
\({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda = \frac{3}{2}\lambda = \frac{3}{2}{.4.10^{ - 7}} = {6.10^{ - 7}}{\mkern 1mu} {\mkern 1mu} \left( m \right)\). Chọn C.
Câu 129:
 Xem đáp án
Xem đáp án
Tốc độ truyền ánh sáng là: \(v = \frac{c}{n} \Rightarrow v\~\frac{1}{n}\)
Vậy tốc độ truyền ánh sáng chậm nhất trong môi trường có chiết suất lớn nhất. Chọn A.
Câu 130:
 Xem đáp án
Xem đáp án
Con lắc đơn có quỹ đạo tròn, ở vị trí cân bằng, tổng hợp lực tác dụng lên con lắc bằng lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\frac{{{v^2}}}{\ell } \to \) A sai.
Khi vật nặng ở vị trí biên, động năng của con lắc: \({W_d} = 0 \Rightarrow W = {W_t} \to \) B đúng.
Dao động của con lắc là dao động điều hòa chỉ khi có biên độ nhỏ → C sai.
Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần → D sai.
Chọn B.
Câu 131:
Một electron chuyển động với vận tốc ban đầu bằng 0, được gia tốc qua một hiệu điện thế 400 V. Tiếp đó, nó được dẫn vào một miền từ trường với vectơ cảm ứng từ vuông góc với vectơ vận tốc của electron. Quỹ đạo của electron là một đường tròn bán kính R = 7 cm. Độ lớn cảm ứng từ là
 Xem đáp án
Xem đáp án
Áp dụng định lí biến thiên động năng cho electron, ta có:
\[{W_{ds}} - {W_{dt}} = A \Rightarrow \frac{1}{2}m{v^2} - 0 = \left| e \right|.U \Rightarrow v = \sqrt {\frac{{2\left| e \right|.U}}{m}} \]
Bán kính chuyển động của electron trong từ trường là:
\[R = \frac{{mv}}{{\left| e \right|B}} = \frac{{m.\sqrt {\frac{{2\left| e \right|U}}{m}} }}{{\left| e \right|.B}} = \frac{1}{B}.\sqrt {\frac{{2m.U}}{{\left| e \right|}}} \Rightarrow B = \frac{1}{R}.\sqrt {\frac{{2m.U}}{{\left| e \right|}}} \]\[ \Rightarrow B = \frac{1}{{{{7.10}^{ - 2}}}}.\sqrt {\frac{{2.9,{{1.10}^{ - 31}}.400}}{{\left| { - 1,{{6.10}^{ - 19}}} \right|}}} \approx 0,{96.10^{ - 3}}{\mkern 1mu} {\mkern 1mu} \left( T \right)\].
Chọn A.
Câu 132:
 Xem đáp án
Xem đáp án
Hiện tượng điện phân không ứng dụng để đúc điện. Chọn C.
Câu 133:
 Xem đáp án
Xem đáp án
Electron chuyển động trong từ trường với quỹ đạo tròn có bán kính là:
\(eBv = \frac{{m{v^2}}}{r} \Rightarrow r = \frac{{mv}}{{eB}} \Rightarrow v = \frac{{e.Br}}{m} = \frac{{1,{{6.10}^{ - 19}}.1,{{88.10}^{ - 4}}}}{{9,{{1.10}^{ - 31}}}} \approx {33.10^6}{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\)
Áp dụng công thức Anh—xtanh về hiện tượng quang điện, ta có:
\(\frac{{hc}}{\lambda } = A + \frac{1}{2}m{v_{0\max }}^2\)\( \Rightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{{{71.10}^{ - 12}}}} = A + \frac{1}{2}.9,{1.10^{ - 31}}.{\left( {{{33.10}^6}} \right)^2}\)
\( \Rightarrow A = 2,{3.10^{ - 15}}{\mkern 1mu} {\mkern 1mu} \left( J \right) = 14,4{\mkern 1mu} {\mkern 1mu} \left( {keV} \right)\). Chọn D.
Câu 134:
Sóng dừng truyền trên sợi dây PQ. Biết P, R, Q là nút sóng. S và T là hai điểm trên dây cách R một khoảng x như hình vẽ. Phát biểu nào sau đây đúng về dao động của hai điểm S và T?
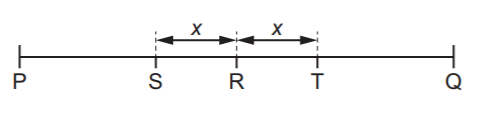
 Xem đáp án
Xem đáp án
Nhận xét: hai điểm S, T đối xứng qua nút sóng\( \to \) S, T dao động ngược pha
Khoảng cách từ S và T tới nút sóng R là: \(RS = RT = x \Rightarrow {A_S} = {A_T}\)
→ Hai điểm S, T dao động cùng biên độ, ngược pha (lệch pha 1800).
Chọn C.
Câu 135:
Một electron được giữ lơ lửng đứng yên giữa hai tấm kim loại cách nhau 5 cm. Hai tấm kim loại được duy trì bởi điện thế lần lượt là +2000 V và -500 V. Lực điện tác dụng lên electron là
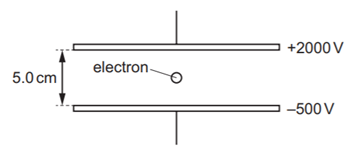
 Xem đáp án
Xem đáp án
Độ lớn hiệu điện thế giữa hai tấm kim loại là:
\[U = \left| {{V_1} - {V_2}} \right| = \left| { + 2000 - \left( { - 500} \right)} \right| = 2500{\mkern 1mu} {\mkern 1mu} \left( V \right)\]
Lực điện tác dụng lên electron là: \[{F_d} = E.e = \frac{U}{d}.e = \frac{{2500}}{{0,05}}.1,{6.10^{ - 19}} = {8.10^{ - 15}}{\mkern 1mu} {\mkern 1mu} \left( N \right)\].
Chọn D.
Câu 136:
Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp (cuộn dây thuần cảm, tụ điện có điện dung C thay đổi được) một điện áp xoay chiều \(u = U\sqrt 2 \cos \omega {\rm{t}}\) (V). Trong đó U và \(\omega \) không đổi. Cho C biến thiên thu được đồ thị biểu diễn điện áp trên tụ theo dung kháng \({{\rm{Z}}_{\rm{C}}}\) như hình vẽ. Coi \(72,11 = 20\sqrt {13} .\) Điện trở của mạch là
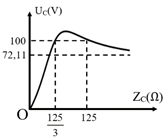
 Xem đáp án
Xem đáp án
Hiệu điện thế giữa hai đầu tụ điện là:
\({U_C} = I.{Z_C} = \frac{{U{Z_C}}}{Z} = \frac{{U{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U{Z_C}}}{{\sqrt {{{\left( {{R^2} + {Z_L}} \right)}^2} - 2{Z_L}{Z_C} + {Z_C}^2} }}\)
\( \Rightarrow {U_C} = \frac{U}{{\sqrt {\left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 1} }}{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Từ (1), ta có: \(\left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 1 - {\left( {\frac{U}{{{U_C}}}} \right)^2} = 0\) (*)
Với giá trị của dung kháng \(\left\{ {\begin{array}{*{20}{l}}{{Z_{{C_1}}} = \frac{{125}}{3}{\mkern 1mu} {\mkern 1mu} \Omega }\\{{Z_{{C_2}}} = 125{\mkern 1mu} {\mkern 1mu} \Omega }\end{array}} \right.\), cho cùng 1 giá trị hiệu điện thế: \({U_{{C_1}}} = {U_{{C_2}}} = 100{\mkern 1mu} {\mkern 1mu} \left( V \right)\)
Khi \({Z_C} \to \infty \) thì \({U_C} = U = 72,11{\mkern 1mu} {\mkern 1mu} V = 20\sqrt {13} {\mkern 1mu} {\mkern 1mu} V\)\( \Rightarrow 1 - {\left( {\frac{U}{{{U_C}}}} \right)^2} = 1 - {\left( {\frac{{20\sqrt {13} }}{{100}}} \right)^2} = 0,48\)
\( \Rightarrow \left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 0,48 = 0\)
Theo định lí Vi – et, đặt \[x = \frac{1}{{{Z_C}}}\] ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{{{Z_{{C_1}}}}} + \frac{1}{{{Z_{{C_2}}}}} = \frac{{2{Z_L}}}{{{R^2} + {Z_L}^2}}}\\{\frac{1}{{{Z_{{C_1}}}}}.\frac{1}{{{Z_{{C_2}}}}} = \frac{{0,48}}{{{R^2} + {Z_L}^2}}}\end{array}} \right.\)
\( \Rightarrow {R^2} + {Z_L}^2 = \frac{{0,48}}{{\frac{1}{{{Z_{{C_1}}}}}.\frac{1}{{{Z_{{C_2}}}}}}} = \frac{{0,48}}{{\frac{1}{{\frac{{125}}{3}}}.\frac{1}{{125}}}} = 2500\)\( \Rightarrow \frac{1}{{\frac{{125}}{3}}} + \frac{1}{{125}} = \frac{{2{Z_L}}}{{2500}} \Rightarrow {Z_L} = 40{\mkern 1mu} {\mkern 1mu} \left( \Omega \right)\)
\( \Rightarrow R = \sqrt {2500 - {{40}^2}} = 30{\mkern 1mu} {\mkern 1mu} \left( \Omega \right)\).
Đáp án: \(30\Omega \)
Câu 137:
Tiến hành cracking và tách hydrogen alkane X thu được hỗn hợp Y gồm có 6 chất gồm alkane mới, alkene, \[{H_2}\]và alkane dư. Đem đốt cháy hoàn toàn hỗn hợp Y trong khí oxygen thu được sản phẩm cháy. Dẫn sản phẩm cháy qua dung dịch nước vôi trong dư thấy xuất hiện 40 gam kết tủa và khối lượng dung dịch giảm 13,4 gam so với ban đầu. Công thức alkane X là
 Xem đáp án
Xem đáp án
Đốt cháy Y cũng giống như đốt cháy X.
\[X{\rm{ }} + {\rm{ }}{O_2} \to {\rm{ }}C{O_2} + {\rm{ }}{H_2}O\]
Ta có: \({n_{C{O_2}}} = {n_{CaC{O_3}}} = 0,4\,mol\)
\( \Rightarrow {n_{{H_2}O}} = \frac{9}{{18}} = 0,5\,mol\)
Đốt cháy alkane X \( \Rightarrow {n_X} = {n_{{H_2}O}} - {n_{C{O_2}}} = 0,5 - 0,4 = 0,1\,mol\)
Gọi công thức phân tử của X là \[{C_n}{H_{2n + 2}}\left( {n{\rm{ }} \ge {\rm{ }}1} \right)\]
Bảo toàn nguyên tố C \(n = \frac{{{n_{C{O_2}}}}}{{{n_X}}} = 4\)
Vậy CTPT của alkane X là \[{C_4}{H_{10}}.\]
Chọn A.
Câu 138:
Xác định độ tan của \[FeS{O_4}\]trong nước ở \[{25^o}C\] biết rằng ở nhiệt độ này khi hòa tan hết 166,8 gam muối ngậm nước \[FeS{O_4}.7{H_2}O\]trong 300 gam \[{H_2}O\]thì thu được dung dịch bão hòa.
 Xem đáp án
Xem đáp án
\(\begin{array}{l}{n_{FeS{O_4}.7{H_2}O}} = \frac{{166,8}}{{278}} = 0,6\,mol = {n_{FeS{O_4}}}\\ \Rightarrow {m_{FeS{O_4}}}\; = 0,6 \cdot 152 = 91,2{\rm{ }}gam\end{array}\)
Khi cho muối ngậm nước vào 300 gam \[{H_2}O\]thì ta có:
\[{m_{{H_2}O}}\; = 300 + 0,6 \cdot 7 \cdot 18 = 375,6{\rm{ }}gam\]
375,6 gam \[{H_2}O\]hòa tan 91,2 gam \[FeS{O_4}\]
→ 100 gam \[{H_2}O\] hòa tan \(\frac{{100 \cdot 91,2}}{{375,6}} \approx 24,28\) gam \[FeS{O_4}\]
Vậy độ tan của \[FeS{O_4}\] ở \[{25^o}C\] là 24,28 gam.
Chọn B.
Câu 139:
Để xác định hàm lượng \[FeC{O_3}\]trong quặng Siderit, người ta làm như sau: Cân 0,6 gam mẫu quặng, chế hóa nó theo một quy trình hợp lí, thu được \[FeS{O_4}\]trong môi trường \[{H_2}S{O_4}\]loãng. Chuẩn độ dung dịch thu được bằng dung dịch chuẩn \[KMn{O_4}\] 0,025M thì dùng vừa hết 25,2 ml. Phần trăm theo khối lượng của \[FeC{O_3}\]là
 Xem đáp án
Xem đáp án
\({n_{KMn{O_4}}} = 0,025 \cdot 25,{2.10^{ - 3}} = 6,{3.10^{ - 4}}\left( {mol} \right)\)
Phản ứng chuẩn độ:
\[10{\rm{ }}FeS{O_4} + {\rm{ }}2KMn{O_4} + {\rm{ }}8{H_2}S{O_4} \to 5{\rm{ }}F{e_2}{\left( {S{O_4}} \right)_3} + {\rm{ }}2MnS{O_4} + {\rm{ }}{K_2}S{O_4} + {\rm{ }}8{H_2}O\]
Theo PTHH: \({n_{F{\rm{eS}}{{\rm{O}}_4}}} = 5{n_{KMn{O_4}}} = 5 \cdot 6,{3.10^{ - 4}} = 3,{15.10^{ - 3}}\left( {mol} \right)\)
Bảo toàn nguyên tố Fe: \({n_{F{\rm{e}}C{{\rm{O}}_3}}} = {n_{F{\rm{eS}}{{\rm{O}}_4}}} = 3,{15.10^{ - 3}}\left( {mol} \right)\)
⟹ \({m_{F{\rm{e}}C{{\rm{O}}_3}}} = 3,{15.10^{ - 3}} \cdot 116 = 0,3654\,\left( g \right)\)
⟹ \(\% {m_{F{\rm{e}}C{{\rm{O}}_3}}} = \frac{{0,3654}}{{0,6}}.100\% = 60,9\% \).
Chọn C.
Câu 140:
Hỗn hợp X gồm 2 chất có công thức phân tử là \[{C_3}{H_{12}}{N_2}{O_3}\]và \[{C_2}{H_8}{N_2}{O_3}.\]Cho 3,40 gam X phản ứng vừa đủ với dung dịch NaOH (đun nóng), thu được dung dịch Y chỉ gồm các chất vô cơ và 0,04 mol hỗn hợp 2 chất hữu cơ đơn chức (đều làm xanh giấy quỳ tím ẩm). Cô cạn Y, thu được m gam muối khan. Giá trị của m là
 Xem đáp án
Xem đáp án
Dung dịch Y chỉ gồm các chất vô cơ ⟹ 2 chất ban đầu là muối của các acid vô cơ (\[{H_2}C{O_3}\]và \[HN{O_3}\]).
Sau phản ứng thu được 2 chất hữu cơ đơn chức (đều làm xanh giấy quỳ tím ẩm) ⟹ 2 chất hữu cơ này là amine.
⟹ X gồm \(\left\{ \begin{array}{l}{\left( {C{H_3}N{H_3}} \right)_2}C{O_3}\;\left( {a{\rm{ }}mol} \right)\\{C_2}{H_5}N{H_3}N{O_3}\;\left( {b{\rm{ }}mol} \right)\end{array} \right.\)
⟹ \[{m_X}\; = {\rm{ }}124a{\rm{ }} + {\rm{ }}108b{\rm{ }} = {\rm{ }}3,4{\rm{ }}\left( 1 \right)\]
\(\)\[\begin{array}{*{20}{l}}{{{\left( {C{H_3}N{H_3}} \right)}_2}C{O_3} + {\rm{ }}2NaOH{\rm{ }} \to {\rm{ }}N{a_2}C{O_3} + {\rm{ }}2C{H_3}N{H_2} \uparrow {\rm{ }} + {\rm{ }}2{H_2}O}\\{\;\;\;\;\;\;\;\;\;\;{\rm{ }}a\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }} \to \;\;\;\;{\rm{ }}a\;\;\;{\rm{ }} \to \;\;\;{\rm{ }}\;\;\;\;2a{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\left( {mol} \right)}\\{{C_2}{H_5}N{H_3}N{O_3} + {\rm{ }}NaOH{\rm{ }} \to {\rm{ }}NaN{O_3} + {\rm{ }}{C_2}{H_5}N{H_2} \uparrow {\rm{ }} + {\rm{ }}{H_2}O}\\{\;\;\;\;\;\;\;\;{\rm{ }}b\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }} \to \;\;\;\;\;{\rm{ }}b\;\;\;\;{\rm{ }} \to \;\;\;\;\;\;\;{\rm{ }}b\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\left( {mol} \right)}\end{array}\]
⟹ \[{n_{a\min e}} = {\rm{ }}2a{\rm{ }} + {\rm{ }}b{\rm{ }} = {\rm{ }}0,04{\rm{ }}\left( 2 \right)\]
Từ (1) và (2) ⟹ a = 0,01; b = 0,02.
Muối khan thu được sau phản ứng gồm: \[N{a_2}C{O_3}\left( {0,01{\rm{ }}mol} \right);{\rm{ }}NaN{O_3}\left( {0,02{\rm{ }}mol} \right)\]
⟹ m = 0,01.106 + 0,02.85 = 2,76 gam.
Chọn D.
Câu 141:
Thí nghiệm xác định định tính nguyên tố carbon và hydrogen trong phân tử saccharose được tiến hành theo các bước sau:
Bước 1: Trộn đều khoảng 0,2 gam saccharose với 1 đến 2 gam copper(II) oxide, sau đó cho hỗn hợp vào ống nghiệm khô (ống số 1) rồi thêm tiếp khoảng 1 gam copper(II) oxide để phủ kín hỗn hợp. Nhồi một nhúm bông có rắc bột \[CuS{O_4}\] khan vào phần trên ống số 1 rồi nút bằng nút cao su có ống dẫn khí.
Bước 2: Lắp ống số 1 lên giá thí nghiệm rồi nhúng ống dẫn khí vào dung dịch \[Ca{(OH)_2}\]đựng trong ống nghiệm (ống số 2).
Bước 3: Dùng đèn cồn đun nóng ống số 1 (lúc đầu đun nhẹ, sau đó đun tập trung vào phần có hỗn hợp phản ứng).
Cho các phát biểu sau:
(a) \[CuS{O_4}\]khan được dùng để nhận biết \[{H_2}O\]sinh ra trong thí nghiệm.
(b) Thí nghiệm trên, trong ống số 2 có xuất hiện kết tủa trắng.
(c) Ở bước 2, lắp ống số 1 sao cho miệng ống hướng lên.
(d) Thí nghiệm trên còn được dùng để xác định định tính nguyên tố oxygen trong phân tử saccharose.
(e) Kết thúc thí nghiệm: tắt đèn cồn, để ống số 1 nguội hẳn rồi mới đưa ống dẫn khí ra khỏi dung dịch trong ống số 2.
Số phát biểu đúng là
 Xem đáp án
Xem đáp án
(a) đúng, nguyên tố H trong saccharose chuyển hoá thành \[{H_2}O\] nên màu trắng của \[CuS{O_4}\] khan chuyển thành màu xanh của \[CuS{O_4}.5{H_2}O.\]
(b) đúng, PTHH: \[C{O_2} + {\rm{ }}Ca{\left( {OH} \right)_2} \to {\rm{ }}CaC{O_3} \downarrow {\rm{ }} + {\rm{ }}{H_2}O.\]
(c) sai, đặt miệng ống nghiệm hơi chúc xuống trên giá ống nghiệm để hơi nước và \[C{O_2}\] thoát ra ống dẫn khí.
(d) sai, thí nghiệm chỉ xác định định tính được C và H.
(e) sai, tháo ống dẫn khí trước khi tắt đèn cồn để tránh dung dịch trong ống 2 bị hút vào ống dẫn khí do áp suất trong ống 1 giảm.
Vậy có 2 phát biểu đúng.
Chọn A.
Câu 142:
Từ 180 gam glucose, bằng phương pháp lên men rượu, thu được a gam ethyl alcohol (hiệu suất 80%). Oxi hoá 0,l a gam ethyl alcohol bằng phương pháp lên men giấm, thu được hỗn hợp X. Để trung hoà hỗn hợp X cần dùng 720 ml dung dịch NaOH 0,2M. Hiệu suất quá trình lên men giấm là:
 Xem đáp án
Xem đáp án
* Xét quá trình lên men rượu
Ta có:
Vì hiệu xuất đạt \(80\% \) lên men rượu \( \Rightarrow {{\rm{n}}_{{{\rm{C}}_2}{{\rm{H}}_s}{\rm{OH}}}} = 2 \cdot 0,8 = 1,6\,\;{\rm{mol}}\).
* Xét quá trình oxi hóa (chú ý lượng ethyl alcohol lấy bằng \(\frac{1}{{10}}\)so với quá trình lên men rượu)

\(\begin{array}{l}{\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{NaOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COONa}} + {{\rm{H}}_2}{\rm{O}}\\0,144 \leftarrow \,\,\,\,\,\,\,\,\,\,0,144\;{\rm{mol}}\end{array}\)
Hiệu xuất phản ứmg: \({\rm{H}}\% = \frac{{0,144}}{{0,16}} \cdot 100\% = 90\% \).
Chọn B.
Câu 143:
Hòa tan hoàn toàn 25,3 gam hỗn hợp X gồm Mg, Al, Zn bằng dung dịch \[HN{O_3}.\] Sau khi phản ứng kết thúc thu được dung dịch Y và 4,48 lít (đktc) khí Z (gồm hai hợp chất khí không màu) có khối lượng 7,4 gam. Cô cạn dung dịch Y thu được 122,3 gam hỗn hợp muối. Số mol \[HN{O_3}\] đã tham gia phản ứng là:
 Xem đáp án
Xem đáp án
Các dữ kiện đề bài có thể tóm tắt lại thành sơ đồ sau:
![Hòa tan hoàn toàn 25,3 gam hỗn hợp X gồm Mg, Al, Zn bằng dung dịch \[HN{O_3}.\] Sau khi phản ứng kết thúc thu được dung dịch Y và 4,48 lít (đktc) khí (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid6-1721814779.png)
Do Z gồm hỗn hợp hai hợp chất khí không màu và có \({\overline M _Z} = \frac{{7,4}}{{0,2}} = 37\)nên không có \[N{O_2}\]:
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{NO:a}\\{{N_2}O:b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 0,2}\\{30a + 44b = 7,4}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 0,1}\\{b = 0,1}\end{array}} \right.} \right.} \right.(mol)\)
Giả sử trong dung dịch Y không có muối \(N{H_4}N{O_3}\)nên ta có:
![Hòa tan hoàn toàn 25,3 gam hỗn hợp X gồm Mg, Al, Zn bằng dung dịch \[HN{O_3}.\] Sau khi phản ứng kết thúc thu được dung dịch Y và 4,48 lít (đktc) khí (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid7-1721814807.png)
Nhận thấy: \(93,5 \ne 122,3\)→ dung dịch Y có muối \(N{H_4}N{O_3}\)
Gọi
![Hòa tan hoàn toàn 25,3 gam hỗn hợp X gồm Mg, Al, Zn bằng dung dịch \[HN{O_3}.\] Sau khi phản ứng kết thúc thu được dung dịch Y và 4,48 lít (đktc) khí (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid8-1721814813.png)
Chọn C.
Câu 144:
Cho một lá iron nhỏ tác dụng với dung dịch \[{H_2}S{O_4}.\]Thể tích khí \[{H_2}\] thu được tương ứng với thời gian đo được như sau:
![Cho một lá iron nhỏ tác dụng với dung dịch \[{H_2}S{O_4}.\]Thể tích khí \[{H_2}\] thu được tương ứng với thời gian đo được như sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid9-1721815075.png)
Trong thời gian 1 phút, lượng H2 thoát ra lớn nhất là bao nhiêu ml?
 Xem đáp án
Xem đáp án
Quan sát đồ thị ta thấy, ở thời điểm từ 2 phút đến 3 phút đường biểu diễn sự phụ thuộc của thể tích khí \[{H_2}\]vào thời gian có độ dốc lớn nhất tức lượng khí \[{H_2}\] được tạo ra là nhiều nhất = 50 - 10 = 40 ml.
Chọn A.
Câu 145:
Để xác định nồng độ dung dịch \[{H_2}{O_2},\]người ta hoà tan 0,5 gam nước oxy già vào nước, thêm \({H_2}S{O_4}\) tạo môi trường acid. Chuẩn độ dung dịch thu được cần vừa đủ 10 ml dung dịch \(KMn{O_4}\) 0,1M thu được các sản phẩm: \[{K_2}S{O_4},{\rm{ }}MnS{O_4},{\rm{ }}{O_2},{\rm{ }}{H_2}O.\] Hàm lượng \[{H_2}{O_2}\]trong nước oxy già là:
 Xem đáp án
Xem đáp án
Ta có: \({n_{KMn{O_4}}} = 0,001\;{\rm{mol}}\)
\(5{{\rm{H}}_2}{{\rm{O}}_2} + 2{\rm{KMn}}{{\rm{O}}_4} + 3{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4} \to {{\rm{K}}_2}{\rm{S}}{{\rm{O}}_4} + 2{\rm{MnS}}{{\rm{O}}_4} + 5{{\rm{O}}_2} + 8{{\rm{H}}_2}{\rm{O }}\)
\({n_{{{\rm{H}}_2}{{\rm{O}}_2}}} = \frac{5}{2}.{n_{{\rm{KMn}}{{\rm{O}}_4}}} = 2,{5.10^{ - 3}}\;{\rm{mol }}\)
\( \Rightarrow \% {m_{{{\rm{H}}_2}{{\rm{O}}_2}}} = \frac{{2,{{5.10}^{ - 3}}.34}}{{0,5}}.100\% = 17\% \)
Chọn B.
Câu 146:
 Xem đáp án
Xem đáp án
Tóm tắt thành sơ đồ sau:
![Hỗn hợp E gồm hai chất hữu cơ X (\[{C_2}{H_7}{O_3}N\]) và Y (\[{C_3}{H_{12}}{O_3}{N_2}\]). X và Y đều có tính chất lưỡng tính. Cho m gam hỗn hợp E tác dụng với dung dịch HCl dư thu được 4,48 lít khí Z (Z là hợp chất vô cơ). Mặt khác, khi cho m gam hỗn hợp E tác dụng với dung dịch NaOH dư, đun nóng thoát ra 6,72 lít khí T (T là hợp chất hữu cơ đơn chức chứa C, H, N và làm xanh giấy quỳ tím ẩm). Cô cạn dung dịch thu được chất rắn gồm hai chất vô cơ. Thể tích các khí đo ở đktc. Giá trị của m là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid10-1721815203.png)
- X và Y đều có 3 nguyên tử O trong phân tử → chúng có thể chứa các gốc \({\rm{C}}{{\rm{O}}_3}^{2 - },{\rm{NO}}_3^ - ,{\rm{HCO}}_3^ - \)
- Khi cho X, Y phản ứng với NaOH thu được khí T chứa C, H, N chứng tỏ khí T là amine, Y lại có 2 nguyên tử N
→ Y có thể là \[C{H_3}N{H_3}C{O_3}N{H_3}C{H_3}\]
- Khi cho X, Y phản ứng với HCl thu được khí Z là chất vô cơ nên Z là \[C{O_2}\]→ X là muối carbonate → X có thể là \[C{H_3}N{H_3}HC{O_3}\]
\( \Rightarrow E\left\{ {\begin{array}{*{20}{l}}{{\rm{C}}{{\rm{H}}_3}{\rm{N}}{{\rm{H}}_3}{\rm{HC}}{{\rm{O}}_3}:a(\;{\rm{mol}})}\\{{\rm{C}}{{\rm{H}}_3}{\rm{N}}{{\rm{H}}_3}{\rm{C}}{{\rm{O}}_3}{\rm{N}}{{\rm{H}}_3}{\rm{C}}{{\rm{H}}_3}:{\rm{b}}({\rm{mol}})}\end{array}} \right.\)
\[ \to {\rm{m}} = 0,1 \cdot 93 + 0,1 \cdot 124 = 21,7\,({\rm{gam}})\]
Đáp án: 21,7
Câu 147:
 Xem đáp án
Xem đáp án
Hoocmôn thực vật (phitôhoocmôn) là các chất hữu cơ do cơ thể thực vật điều tiết hoạt động sống của cây. Khác với enzim là chất xúc tác cho 1 phản ứng sinh hoá, hoocmôn hoạt hoá cả 1 chương trình phát sinh hình thái như kích thích hạt và chồi nảy mầm - gồm rất nhiều quá trình và nhiều phản ứng sinh hoá. Chọn A.
Câu 148:
 Xem đáp án
Xem đáp án
Giun đất trao đổi khí với môi trường qua da nên da của giun đất cần ẩm ướt để \({{\rm{O}}_2},{\rm{C}}{{\rm{O}}_2}\) có thể hòa tan và khuếch tán qua da được dễ dàng. Nếu bắt giun đất để trên bề mặt đất khô ráo, da sẽ bị khô nên giun không hô hấp được và sẽ bị chết. Chọn C.
Câu 149:
 Xem đáp án
Xem đáp án
Thụ tinh chéo có sự tổ hợp vật chất di truyền từ hai nguồn khác nhau nên có tính biến dị đa dạng hơn, tạo tính đa dạng ở đời con nên khả năng thích nghi cao hơn. Tự thụ tinh làm cho cá thể đời con thuần chủng nên hạn chế nguồn biến dị tổ hợp. Chọn A.
Câu 150:
Hình bên dưới thể hiện cấu trúc của một số loại nuclêôtit cấu tạo nên ADN và ARN.
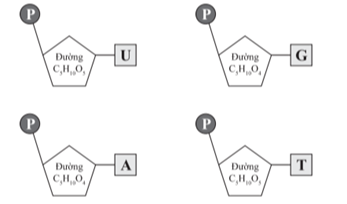
Hình nào trong số các hình trên là không phù hợp?
 Xem đáp án
Xem đáp án
T là bazơ nitơ trong ADN nên phải có đường đêôxiribôzơ \({\rm{(}}{{\rm{C}}_5}{{\rm{H}}_{10}}{{\rm{O}}_4}).\) Chọn D.
Câu 151:
 Xem đáp án
Xem đáp án
Dạng đột biến cấu trúc NST làm tăng hoạt tính của enzim amilaza ở đại mạch là lặp đoạn. Chọn D.
Câu 152:
Từ cây có kiểu gen AaBb, bằng phương pháp nuôi cấy hạt phấn trong ống nghiệm có thể tạo ra tối đa bao nhiêu dòng cây đơn bội có kiểu gen khác nhau?
 Xem đáp án
Xem đáp án
Kiểu gen AaBb bình thường giảm phân cho ra 4 loại giao tử đơn bội, nuôi cấy sẽ tạo ra tối đa 4 dòng cây đơn bội. Chọn D.
Câu 153:
Một quần thể thực vật tự thụ phấn, xét 1 gen có 2 alen là B và b. Theo lí thuyết, quần thể có cấu trúc di truyền nào sau đây có tần số các kiểu gen không đổi qua các thế hệ?
 Xem đáp án
Xem đáp án
Quần thể chỉ gồm các kiểu gen thuần chủng khi tự thụ phấn sẽ có cấu trúc di truyền không đổi qua các thế hệ. Do đó, trong các quần thể đã cho, quần thể có cấu trúc di truyền là 100% bb sẽ có tần số các kiểu gen không đổi qua các thế hệ. Chọn B.
Câu 154:
 Xem đáp án
Xem đáp án
Bằng chứng sinh học phân tử gồm: trình tự axit amin, trình tự nuclêôtit,… Chọn D.
A là bằng chứng hóa thạch, C là bằng chứng giải phẫu so sánh, D là bằng chứng tế bào học.
Câu 155:
Hình dưới đây minh hoạ tốc độ sinh trưởng giả định của ba loài cây ngập mặn thân gỗ lâu năm kí hiệu là loài (I), (II) và (III) tương ứng với các điều kiện độ mặn khác nhau. Số liệu trong bảng dưới đây cho biết độ mặn cao nhất tại ba bãi lầy ven biển A, B và C của địa phương H. Giả sử các điều kiện sinh thái khác của ba bãi lầy này là tương đồng nhau, không ảnh hưởng đến sức sống của các loài cây này và sự sai khác về độ mặn giữa các vị trí trong mỗi bãi lầy là không đáng kể. Các cây con của ba loài này khi trồng không thể sống được ở các dải độ mặn có tốc độ sinh trưởng bằng 0.
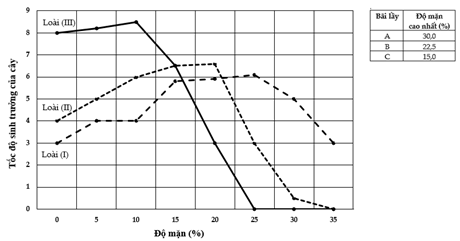
Địa phương H có kế hoạch trồng các loài cây (I), (II) và (III) để phục hồi rừng ngập mặn ở ba bãi lầy A, B và C. Dựa vào thông tin trong hình và bảng, có bao nhiêu nhận định sau đây đúng giúp địa phương H lựa chọn các loài cây này cho phù hợp?
I. Loài (I) có khả năng chịu độ mặn cao nhất trong ba loài.
II. Tốc độ sinh trưởng của loài (II) tỉ lệ nghịch với độ mặn của cả ba bãi lầy.
III. Bãi lầy B và C trồng xen được hai loài (I) và (II), bãi lầy A trồng xen được cả ba loài.
IV. Loài (III) có tốc độ sinh trưởng lớn hơn loài (I) và loài (II) ở độ mặn từ 22,5% đến 35%.
 Xem đáp án
Xem đáp án
I. Đúng. Thứ tự chịu mặn: Loài (I) > loài (II) > Loài (III).
II. Sai. Tốc độ sinh trưởng của loài (II) không tỉ lệ nghịch với độ mặn của cả ba bãi lầy mà có lúc tăng có lúc giảm.
III. Sai. Bãi lầy B và C trồng xen được cả 3 loài là (I), (II), (III); bãi lầy A chỉ trồng xen được hai loài là (I) và (II).
IV. Sai. Loài (III) có tốc độ sinh trưởng kém hơn loài (I) và loài (II) ở độ mặn từ 22,5% đến 35%.
Chọn D.
Câu 156:
Ở ruồi giấm, xét 3 cặp gen: A, a; B, b và D, d; mỗi gen quy định 1 tính trạng, các alen trội là trội hoàn toàn. Phép lai P: 2 ruồi đều có kiểu hình trội về 3 tính trạng giao phối với nhau, tạo ra F1 gồm 24 loại kiểu gen và có 1,25% số ruồi mang kiểu hình lặn về 3 tính trạng nhưng kiểu hình này chỉ có ở ruồi đực. Theo lí thuyết, trong tổng số ruồi cái có kiểu hình trội về 3 tính trạng ở F1, số ruồi có 5 alen trội chiếm tỉ lệ là bao nhiêu?
 Xem đáp án
Xem đáp án
F1 thu được 24 loại kiểu gen mà kiểu hình lặn về 3 tính trạng chiếm 1,25% chỉ có ở giới đực ® Gen nằm trên NST giới tính X tại vùng không tương đồng.
TH1: Xét 1 gen nằm trên giới tính (ví dụ gen Dd)
Ta có: XDXd × XDY ® XdY = 0,25 ® (aa, bb) = 1,25% : 0,25 = 5% = 10% ab (ruồi giấm cái) × 50% ab (ruồi giấm đực – ruồi giấm đực không hoán vị gen). Vậy ab (ruồi giấm cái) = 10% suy ra kiểu gen của ruồi giấm cái là \[\frac{{Ab}}{{aB}}\]. Vậy P là \[\frac{{Ab}}{{aB}}\] XDXd (f = 20%) × \[\frac{{AB}}{{ab}}\]XDY . Thử lại, số loại kiểu gen = 7 × 4 = 28 (không thỏa mãn).
Vậy 2 gen nằm trên 1 cặp NST giới tính (ví dụ gen Bb, Dd).
Số loại kiểu gen = 24 = 3 × 8 (cặp Aa có 3 kiểu gen; cặp Bb, Dd có 8 kiểu gen).
Phép lai gen Aa = Aa × Aa ® aa = 0,25 ® XbdY = 5% ® Xbd = 10%.
® F1: AaXBdXbD × AaXBDY.
® Ruồi cái A-B-D- ở F1 = 0,75 × 1/2 = 0,375.
Xác định tỉ lệ ruồi cái có 5 alen trội ở F1:
+ Ruồi cái AA cần 3 alen trội cặp BD (XBDXBd và XBDXbD)\( = \frac{1}{4} \times (0,5 \times 0,4 + 0,5 \times 0,4) = 0,1.\)
+ Ruồi cái Aa cần 4 alen trội cặp BD (XBDXBD) \( = \frac{2}{4} \times (0,5 \times 0,1) = 0,025.\)
Vậy tỉ lệ cần tìm = \[\frac{{0,1 + 0,025}}{{0,375}} = \frac{1}{3}.\] Đáp án: \(\frac{1}{3}.\)
