Thí nghiệm xác định định tính nguyên tố carbon và hydrogen trong phân tử saccharose được tiến hành theo các bước sau:
Bước 1: Trộn đều khoảng 0,2 gam saccharose với 1 đến 2 gam copper(II) oxide, sau đó cho hỗn hợp vào ống nghiệm khô (ống số 1) rồi thêm tiếp khoảng 1 gam copper(II) oxide để phủ kín hỗn hợp. Nhồi một nhúm bông có rắc bột \[CuS{O_4}\] khan vào phần trên ống số 1 rồi nút bằng nút cao su có ống dẫn khí.
Bước 2: Lắp ống số 1 lên giá thí nghiệm rồi nhúng ống dẫn khí vào dung dịch \[Ca{(OH)_2}\]đựng trong ống nghiệm (ống số 2).
Bước 3: Dùng đèn cồn đun nóng ống số 1 (lúc đầu đun nhẹ, sau đó đun tập trung vào phần có hỗn hợp phản ứng).
Cho các phát biểu sau:
(a) \[CuS{O_4}\]khan được dùng để nhận biết \[{H_2}O\]sinh ra trong thí nghiệm.
(b) Thí nghiệm trên, trong ống số 2 có xuất hiện kết tủa trắng.
(c) Ở bước 2, lắp ống số 1 sao cho miệng ống hướng lên.
(d) Thí nghiệm trên còn được dùng để xác định định tính nguyên tố oxygen trong phân tử saccharose.
(e) Kết thúc thí nghiệm: tắt đèn cồn, để ống số 1 nguội hẳn rồi mới đưa ống dẫn khí ra khỏi dung dịch trong ống số 2.
Số phát biểu đúng là
 Giải bởi Vietjack
Giải bởi Vietjack
(a) đúng, nguyên tố H trong saccharose chuyển hoá thành \[{H_2}O\] nên màu trắng của \[CuS{O_4}\] khan chuyển thành màu xanh của \[CuS{O_4}.5{H_2}O.\]
(b) đúng, PTHH: \[C{O_2} + {\rm{ }}Ca{\left( {OH} \right)_2} \to {\rm{ }}CaC{O_3} \downarrow {\rm{ }} + {\rm{ }}{H_2}O.\]
(c) sai, đặt miệng ống nghiệm hơi chúc xuống trên giá ống nghiệm để hơi nước và \[C{O_2}\] thoát ra ống dẫn khí.
(d) sai, thí nghiệm chỉ xác định định tính được C và H.
(e) sai, tháo ống dẫn khí trước khi tắt đèn cồn để tránh dung dịch trong ống 2 bị hút vào ống dẫn khí do áp suất trong ống 1 giảm.
Vậy có 2 phát biểu đúng.
Chọn A.
Một hội trường A của một trường Đại học có 600 chỗ ngồi và các hàng ghế được xếp theo dạng bậc thang, hàng ghế đầu tiên có 15 chỗ ngồi và cao \[0,3{\rm{ }}m\] so với mặt nền. Mỗi hàng ghế sau có thêm 3 chỗ ngồi và cao hơn \[0,2{\rm{ }}m\] so với hàng ghế ngay trước nó. Hỏi hàng ghế cuối cùng của hội trường đó sẽ cao bao nhiêu mét so với mặt nền?
Trong không gian \[Oxyz,\] phương trình mặt cầu đi qua điểm \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ là
Từ 180 gam glucose, bằng phương pháp lên men rượu, thu được a gam ethyl alcohol (hiệu suất 80%). Oxi hoá 0,l a gam ethyl alcohol bằng phương pháp lên men giấm, thu được hỗn hợp X. Để trung hoà hỗn hợp X cần dùng 720 ml dung dịch NaOH 0,2M. Hiệu suất quá trình lên men giấm là:
Cho hàm số Biết rằng đồ thị hàm số đã cho đi qua điểm \(\left( { - 1\,;\,\,7} \right)\) và giao điểm hai đường tiệm cận là \(\left( { - 2\,;\,\,3} \right).\) Giá trị của biểu thức \(\frac{{2a + 3b + 4c + d}}{{7c}}\) bằng\(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Hình dưới đây minh hoạ tốc độ sinh trưởng giả định của ba loài cây ngập mặn thân gỗ lâu năm kí hiệu là loài (I), (II) và (III) tương ứng với các điều kiện độ mặn khác nhau. Số liệu trong bảng dưới đây cho biết độ mặn cao nhất tại ba bãi lầy ven biển A, B và C của địa phương H. Giả sử các điều kiện sinh thái khác của ba bãi lầy này là tương đồng nhau, không ảnh hưởng đến sức sống của các loài cây này và sự sai khác về độ mặn giữa các vị trí trong mỗi bãi lầy là không đáng kể. Các cây con của ba loài này khi trồng không thể sống được ở các dải độ mặn có tốc độ sinh trưởng bằng 0.
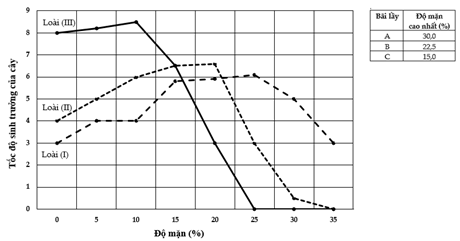
Địa phương H có kế hoạch trồng các loài cây (I), (II) và (III) để phục hồi rừng ngập mặn ở ba bãi lầy A, B và C. Dựa vào thông tin trong hình và bảng, có bao nhiêu nhận định sau đây đúng giúp địa phương H lựa chọn các loài cây này cho phù hợp?
I. Loài (I) có khả năng chịu độ mặn cao nhất trong ba loài.
II. Tốc độ sinh trưởng của loài (II) tỉ lệ nghịch với độ mặn của cả ba bãi lầy.
III. Bãi lầy B và C trồng xen được hai loài (I) và (II), bãi lầy A trồng xen được cả ba loài.
IV. Loài (III) có tốc độ sinh trưởng lớn hơn loài (I) và loài (II) ở độ mặn từ 22,5% đến 35%.
Trong không gian \[Oxyz,\] cho hai vectơ \(\vec a = \left( {2\,;\,\,m - 1\,;\,\,3} \right)\) và \(\vec b = \left( {1\,;\,\,3\,;\,\, - 2n} \right).\) Giá trị của \[m,\,\,n\] để hai vectơ \(\vec a,\,\,\vec b\) cùng hướng với nhau là
Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất \[0,65\% \] một tháng theo phương thức lãi kép. Hỏi sau bao nhiêu lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Văn học Việt Nam từ năm 1945 đến năm 1975 đã _________ và _________ mạnh mẽ những yếu tố truyền thống tư tưởng lớn của dân tộc: chủ nghĩa nhân đạo, đặc biệt là chủ nghĩa yêu nước và chủ nghĩa anh hùng.
Có bao nhiêu số thực \(a\) để \(\int\limits_0^1 {\frac{x}{{a + {x^2}}}{\rm{d}}x} \; = 1\)?
Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} - 1\) với \(a\) là tham số thực. Nếu \[{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = f\left( 1 \right)\] thì \({\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right)\) bằng