Giải bởi Vietjack
Cách 1: Ta có mặt phẳng \((\alpha )\) nhận vectơ \(\overrightarrow {{n_\alpha }} = \left( {1\,;\,\,1\,;\,\,1} \right)\) là vectơ pháp tuyến, đường thẳng \(d\) đi qua điểm \(A\left( {0\,;\,\, - 1\,;\,\,2} \right)\) và nhận \(\overrightarrow {{u_d}} = \left( {1\,;\,\,2\,;\,\, - 1} \right)\) là vectơ chỉ phương.
Gọi \(\left( \beta \right)\) là mặt phẳng chứa đường thẳng \(d\) và vuông góc với mặt phẳng \(\left( \alpha \right).\)
Ta có \(\overrightarrow {{n_\beta }} = \overrightarrow {{n_\alpha }} \wedge \overrightarrow {{n_d}} = \left( { - 3\,;\,\,2\,;\,\,1} \right).\)
Khi đó đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Do đó một vectơ chỉ phương của đường thẳng \(\Delta \) là \(\overrightarrow {{u_\Delta }} = \overrightarrow {{u_\alpha }} \wedge \overrightarrow {{u_\beta }} = \left( { - 1\,;\,\, - 4\,;\,\,5} \right).\)
Mà \(\vec u = \left( {1\,;\,\,a\,;\,\,b} \right)\) nên \(a = 4,\,\,b = - 5.\) Vậy \(a + b = - 1.\)
Cách 2: Dễ dàng tính được tọa độ giao điểm của đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\) là \(I = \left( {1\,;\,\,1\,;\,\,1} \right).\)
Trên đường thẳng lấy điểm \(A\left( {0\,;\,\, - 1\,;\,\,2} \right)\) và gọi \(H\) là hình chiếu vuông góc của \(A\) trên mặt phẳng \((\alpha ).\)
Phương trình đường thẳng đi qua \(A\) và \(H\) có dạng: \(\left\{ {\begin{array}{*{20}{l}}{x = 0 + t}\\{y = - 1 + t}\\{z = 2 + t}\end{array}} \right.\)
Tọa độ của \(H\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 0 + t}\\{y = - 1 + t}\\{z = 2 + t}\\{x + y + z - 3 = 0}\end{array} \Rightarrow t = \frac{2}{3}} \right..\) Do đó \(H\left( {\frac{2}{3}\,;\,\,\frac{{ - 1}}{3}\,;\,\,\frac{8}{3}} \right).\)
Đường thẳng \(\Delta \) đi qua hai điểm \(I\) và \(H\) nhận vectơ \(\overrightarrow {IH} = \left( {\frac{{ - 1}}{3}\,;\,\,\frac{{ - 4}}{3}\,;\,\,\frac{5}{3}} \right)\) là vectơ chỉ phương nên cũng nhận vectơ \(\overrightarrow {{u_\Delta }} = \left( {1\,;\,\,4\,;\,\, - 5} \right)\) là vectơ chỉ phương.
Vậy \(a + b = - 1.\) Chọn C.
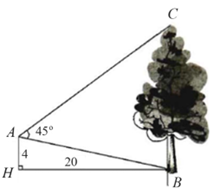
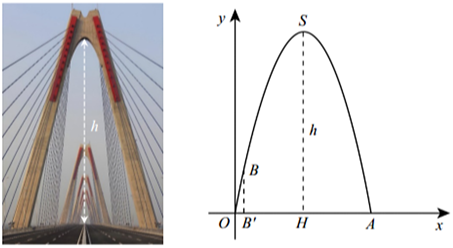
Giả sử rằng mặt trong của trụ cầu là một parabol như vẽ, biết độ rộng của mặt đường khoảng \[43{\rm{ }}m.\] Một người đã dùng dây dọi (không giãn) gắn lên thành trụ cầu ở vị trí \[B\] và điều chỉnh độ dài dây dọi để quả nặng vừa chạm đất (khi lặng gió), sau đó đo được chiều dài đoạn dây dọi sử dụng là \[1,87{\rm{ }}m\] và khoảng cách từ chân trụ cầu đến quả nặng là \[20{\rm{ }}cm.\] Nếu dùng dữ liệu tự thu thập được và tính toán theo cách ở trên thì người này sẽ ước tính được độ cao từ đỉnh vòm phía trong một trụ của cầu Nhật Tân tới mặt đường là bao nhiêu mét (làm tròn đến hàng đơn vị)?
Đáp án: ……….
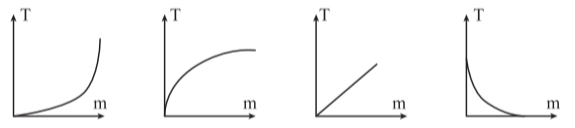
Đồ thị dao động nào sau đây biểu diễn sự phụ thuộc của chu kì T vào khối lượng m của con lắc lò xo đang dao động điều hòa?
Đọc đoạn trích sau và trả lời câu hỏi:
Làm chi để tiếng về sau,
Nghìn năm ai có khen đâu Hoàng Sào!
Sao bằng lộc trọng quyền cao,
Công danh ai dứt lối nào cho qua?
Nghe lời nàng nói mặn mà.
(Truyện Kiều – Nguyễn Du)
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Qua truyện ngắn Chiếc thuyền ngoài xa, Nguyễn Minh Châu đã gửi gắm thông điệp: Nhà văn cần phải thường xuyên xâm nhập đời sống thực tế của xã hội.
