 Giải bởi Vietjack
Giải bởi Vietjack
+ Độ dãn của lò xo tại vị trí cân bằng \(\Delta \ell = \frac{{{\rm{mg}}}}{{\rm{k}}} = \frac{{{{\rm{T}}^2}\;{\rm{g}}}}{{4{{\rm{\pi }}^2}}} = \frac{{0,{5^2}.10}}{{4.10}} = 0,0625\;{\rm{m}} = 6,25\;{\rm{cm}}{\rm{.}}\)
+ Biên độ \({\rm{A}} = 12,5\;{\rm{cm}}{\rm{.}}\)
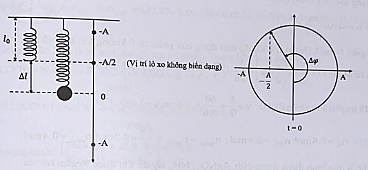
Thấy \(\Delta \ell < {\rm{A}} \Rightarrow \) Lực đàn hồi có độ lớn cực tiểu tại vị trí lò xo không biến dạng \({\rm{x}} = - \Delta \ell = - \frac{{\rm{A}}}{2}\).
Thời gian ngắn nhất kể từ \(t = 0\) đến khi lực đàn hời của lò xo có độ lớn cực tiểu: \(\Delta t = \frac{{\Delta {\rm{\varphi }}}}{{\rm{\omega }}}\).
Từ vòng tròn lượng giác, ta có \(\Delta {\rm{\varphi }} = \frac{{7{\rm{\pi }}}}{6} \Rightarrow \Delta t = \frac{{\frac{{7{\rm{\pi }}}}{6}}}{{\frac{{2{\rm{\pi }}}}{{0,5}}}} = \frac{7}{{24}}s\). Chọn C.
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để đồ thị hàm số \(y = \frac{{x - 1}}{{{x^2} - 8x + m}}\) có 3 đường tiệm cận?
Tất cả giá trị của tham số \(m\) để đồ thị hàm số \(y = {x^3} + \left( {{m^2} - 2} \right)x + 2{m^2} + 4\) cắt các trục tọa độ \[Ox,\,\,Oy\] lần lượt tại \[A,\,\,B\] sao cho diện tích tam giác \[OAB\] bằng 8 là
Thực hiện phản ứng điều chế isoamyl acetate (dầu chuối) theo trình tự sau:
- Bước 1: Cho \(2{\rm{ml}}\) isoamyl alcohol, \(2{\rm{ml}}\) acetic acid nguyên chất và 2 giọt sulfuric acid đặc vào ống nghiệm khô.
- Bước 2: Lắc đều, đun cách thủy hỗn hợp 8-10 phút trong nồi nước sôi.
- Bước 3: Làm lạnh, sau đó rót \(2{\rm{ml}}\) dung dịch \({\rm{NaCl}}\) bão hòa vào ống nghiệm.
Phát biểu nào sau đây sai?
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( {1\,;\,\,2\,;\,\, - 2} \right)\) và \(B\left( {\frac{8}{3}\,;\,\,\frac{4}{3}\,;\,\,\frac{8}{3}} \right).\) Biết \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm của đường tròn nội tiếp tam giác \[OAB.\] Giá trị \(a - b + c\) bằng
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a,{\rm{ }}SA\] vuông góc với đáy và \(SA = a\sqrt 3 .\) Gọi \(\alpha \) là góc giữa \[SD\] và \(\left( {SAC} \right).\) Giá trị \(\sin \alpha \) bằng