Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {y + 1} \right) = xy + 4\\\left( {x + 2} \right)\left( {y - 1} \right) = xy - 10\end{array} \right..\] Nghiệm của hệ phương trình trên là
A. \[\left( {x;y} \right) = \left( {2;3} \right).\]
B. \[\left( {x;y} \right) = \left( {2; - 3} \right).\]
C. \[\left( {x;y} \right) = \left( { - 2; - 3} \right).\]
D. \[\left( {x;y} \right) = \left( { - 2;3} \right).\]
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {y + 1} \right) = xy + 4\\\left( {x + 2} \right)\left( {y - 1} \right) = xy - 10\end{array} \right.\]
Hay \[\left\{ \begin{array}{l}xy + x - y - 1 = xy + 4\\xy - x + 2y - 2 = xy - 10\end{array} \right.\]
Khi đó \[\left\{ \begin{array}{l}x - y = 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\ - x + 2y = - 8\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Để tìm được nghiệm của hệ phương trình trên, ta có hai cách như sau:
⦁ Cách 1. Sử dụng máy tính cầm tay, lần lượt bấm các phím
Trên màn hình hiện lên kết quả \(x = 2\), ta ấn tiếp phím = thì màn hình hiện lên kết quả \(y = - 3\).
Như vậy cặp số \[\left( {2; - 3} \right)\] là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}x - y = 5\\ - x + 2y = - 8\end{array} \right.\].
Vậy ta chọn phương án B.
⦁ Cách 2. Giải hệ phương trình:
Cộng từng vế của hai phương trình của hệ, ta được: \[y = - 3.\]
Thay \[y = - 3\] vào phương trình (1), ta được: \[x - \left( { - 3} \right) = 5\] hay \[x = 2.\]
Vậy hệ phương trình đã cho có nghiệm là \[\left( {x;y} \right) = \left( {2; - 3} \right).\]
Do đó ta chọn phương án B.
Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím:
I. Nhận biết
Điều kiện xác định của phương trình \[\frac{1}{x} - \frac{2}{3} = \frac{{5{x^2}}}{{x - 4}}\] là
Hệ số \[a,b\] và \[c\] tương ứng của phương trình bậc nhất hai ẩn \[ - 7x - 12 = 0\] là:
Cho hệ phương trình \[\left\{ \begin{array}{l}2x + 9y = 10\\5y - 3x = - 6\end{array} \right.,\] hệ số \[a,b,c\] và \[a',b',c'\] của hệ phương trình theo dạng hệ hai phương trình bậc nhất một ẩn là là
Hai ngăn của một kệ sách có tổng cộng \[500\] cuốn sách. Nếu chuyển \[75\] cuốn sách từ ngăn thứ nhất sang ngăn thứ hai thì số sách ở ngăn thứ hai gấp \[3\] lần số sách ở ngăn thứ nhất. Khi đó số sách ở ngăn thứ nhất và ngăn thứ hai ban đầu lần lượt là
Cặp số \[\left( {1; - 5} \right)\] là nghiệm của hệ phương trình nào trong các hệ phương trình sau đây?
Cho hệ phương trình \[\left\{ \begin{array}{l} - x - 3y = 2\\5x + 9y = - 11\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp thế (biểu diễn \(x\) theo \(y)\), ta được phương trình ẩn \(y\) là
III. Vận dụng
Cho phương trình \[\frac{1}{{x + 1}} - \frac{{2{x^2} - m}}{{{x^3} + 1}} = \frac{4}{{{x^2} - x + 1}}.\] Biết \[x = 0\] là một nghiệm của phương trình. Nghiệm còn lại là
II. Thông hiểu
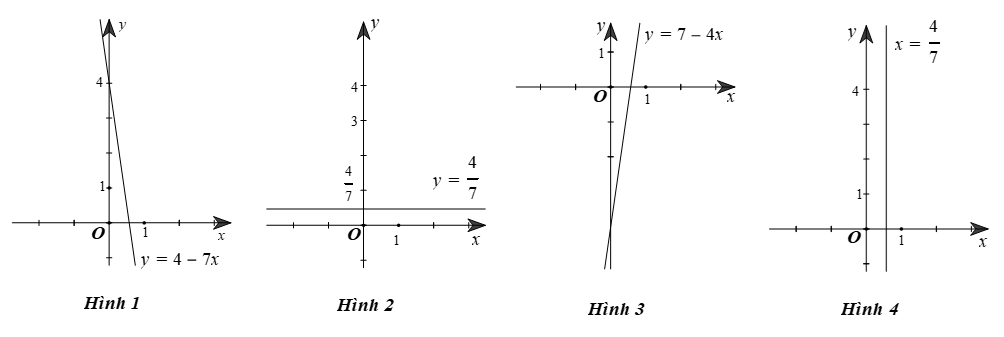
Mỗi nghiệm của phương trình \[7x + 0y = 4\] được biểu diễn bởi một điểm nằm trên đường thẳng có đồ thị là hình vẽ nào trong các hình vẽ sau?
Điểm \[M\left( {1;3} \right)\] không thuộc đường thẳng nào sau đây?
Với giá trị dương nào của \[m\] thì phương trình \[2x - {\left( {m - 2} \right)^2}y = 5\] nhận cặp số \[\left( { - 10; - 1} \right)\] làm nghiệm?
Với giá trị nào của \[{x_0}\] để cặp số \[\left( {{x_0}; - 2} \right)\] là nghiệm của phương trình \[x - 7y = 21?\]
