Cho bát giác đều \[ABCDEFGH\] có tâm \[O.\] Phép quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm nào?
A. \[G.\]
B. \[A.\]
C. \[E.\]
D. \[H.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
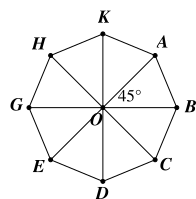
Giả sử \[ABCDEGHK\] là bát giác đều có tâm \[O.\]
Do đó \[AB = BC = CD = DE = EG = GH = HK\] và \[OA = OB = OC = OD = OE = OG = OH = OK.\]
Xét \[\Delta OAB\] và \[\Delta OBC\] có: \[OA = OB,{\rm{ }}OB = OC,{\rm{ }}AB = BC\].
Do đó \[\Delta OAB = \Delta OBC\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right)\].
Tương tự, ta sẽ chứng minh được:
\[\Delta OAB = \Delta OBC = \Delta COD = \Delta DOE = \Delta EOG = \Delta GOH = \Delta HOK = \Delta KOA.\]
Suy ra các góc tương ứng bằng nhau:
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOG} = \widehat {GOH} = \widehat {HOK} = \widehat {KOA}.\)
Ta có: \(\widehat {AOB} + \widehat {BOC} + \widehat {COD} + \widehat {DOE} + \widehat {EOG} + \widehat {GOH} + \widehat {HOK} + \widehat {KOA} = 360^\circ \)
Suy ra \(8\widehat {AOB} = 360^\circ ,\) nên \(\widehat {AOB} = 45^\circ .\)
Do đó, \(\widehat {DOE} = \widehat {EOG} = \widehat {GOH} = 45^\circ .\)
Như vậy, ta sẽ có \[\widehat {DOG} = \widehat {DOE} + \widehat {EOF} + \widehat {FOG} = 45^\circ + 45^\circ + 45^\circ = 135^\circ .\]
Vậy quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm \[G.\]
Do đó ta chọn phương án A.
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Các phép quay tâm \[O\] giữ nguyên hình ngũ giác đều là
III. Vận dụng
Cho lục giác đều \[ABCDEF\] tâm \[O.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[EF,{\rm{ }}BD.\] Khẳng định nào sau đây là sai?
Cho tam giác đều \[ABC\], các đường cao \[AD{\rm{ }},{\rm{ }}BE{\rm{ }},{\rm{ }}CF\] cắt nhau tại H . Gọi \[I{\rm{ }},{\rm{ }}K{\rm{ }},{\rm{ }}M\] theo thứ tự là trung điểm của \[HA{\rm{ }},{\rm{ }}HB{\rm{ }},{\rm{ }}HC\]. Khẳng định nào sau đây là đúng?
Cho hình vuông \[ABCD\] tâm \[O.\] Phép quay ngược chiều 180° tâm O biến các điểm \[A,\,\,B,\,\,C,\,\,D\] thành các điểm nào?
Phép quay với \[O\] là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc
Phép quay giữ nguyên hình đa giác đều \[{A_1}{A_2}{A_3}...{A_n}\,\,\left( {n \ge 3,{\rm{ }}n \in \mathbb{N}} \right)\] là
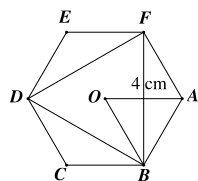
Cho lục giác đều \[ABCDEF\] tâm \(O\) biết \[OA = 4{\rm{ cm}}.\] Độ dài mỗi cạnh của lục giác đều \[ABCDEF\] là bao nhiêu?
Cho đa giác đều 9 cạnh có tâm \[O\] và \[AB,{\rm{ }}BC\] là hai cạnh của đa giác (như hình vẽ).
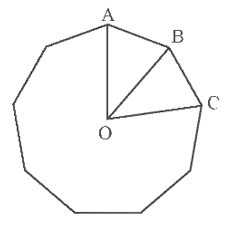
Số đo các góc \[\widehat {AOB}\,,\,\,\widehat {ABO}\,,\,\,\widehat {ABC}\] lần lượt là
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?