A.
B.
C.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Đổi sang
- Trong (ABCD) kẻ trong (SHE) kẻ , chứng minh
- Xác định góc giữa SC và (ABCD), từ đó tính SH.
- Sử dụng từ đó tính HE.
- Sử dụng hệ thức lượng trong tam giác vuông tính HN.
Cách giải:
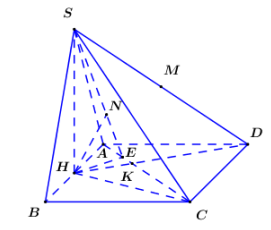
Gọi H là trung điểm AB. Vì cân tại S nên
Ta có:
Gọi Áp dụng định lí Ta-lét ta có:
Ta có
.
Lại có nên .
Do đó .
Trong (ABCD) kẻ , trong (SHE) kẻ ta có:
Vì nên HC là hình chiếu vuông góc của SC lên (ABCD).
.
vuông tại
Ta có:
Áp dụng hệ thức lượng trong tam giác vuông SHE ta có:
Nên .
Vậy
Chọn A.
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
Hàm số y = f(x) liên tục trên [2; 9]. F(x) là một nguyên hàm của hàm số f(x) trên [2; 9] và Mệnh đề nào sau đây đúng?
Cho hàm số y = f(x) có đạo hàm . Số điểm cực tiểu của hàm số đã cho là
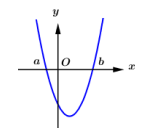
Cho hàm số bậc ba y = f(x) có đồ thị của hàm số f'(x) như hình vẽ và f(b) = 1. Số giá trị nguyên của để hàm số có đúng 5 điểm cực trị là:
Hình trụ tròn xoay có độ dài đường sinh bằng l và bán kính đáy bằng R có diện tích xung quanh cho bởi công thức