Cho hàm số y = f(x) có đạo hàm trên hàm số y = f'(x) liên tục trên hàm số cắt trục hoành tại các điểm có hoành độ a, b, c là các số nguyên và có đồ thị như hình vẽ.
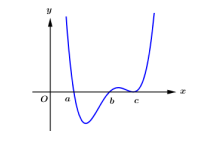
Gọi là số giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng (1; 2); là số giá trị nguyên của tham số m để hàm số đồng biến trên khoảng (1; 2). Khi đó bằng:
A. 2b - 2a + 1
B. 2b - 2a - 2
C. 2b - 2a + 2
D. 2b - 2a
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Xác định khoảng của x ứng với
- Hàm số y = g(x) nghịch biến trên khoảng (1; 2) nên .
- Đưa về bài toán giải các bất phương trình nghiệm đúng. Từ đó tìm
- Tương tự với hàm số h(x) tìm
Cách giải:
Dựa vào đồ thị hàm số ta thấy
Xét hàm số có
Vì y = g(x) nghịch biến trên khoảng (1; 2) nên
Xét
Hàm số đồng biến trên [1; 2] do đó
Tương tự ta có
Từ (1) và (2) ta có
Chứng minh tương tự với hàm h(x) ta có
Vậy
Chọn D.
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
Hàm số y = f(x) liên tục trên [2; 9]. F(x) là một nguyên hàm của hàm số f(x) trên [2; 9] và Mệnh đề nào sau đây đúng?
Cho hàm số y = f(x) có đạo hàm . Số điểm cực tiểu của hàm số đã cho là
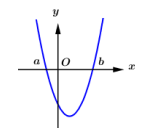
Cho hàm số bậc ba y = f(x) có đồ thị của hàm số f'(x) như hình vẽ và f(b) = 1. Số giá trị nguyên của để hàm số có đúng 5 điểm cực trị là:
Hình trụ tròn xoay có độ dài đường sinh bằng l và bán kính đáy bằng R có diện tích xung quanh cho bởi công thức