Tìm các giá trị của tham số m để \[2{x^2} - 2(m + 1)x + {m^2} - 2m + 4 \ge 0(\forall x)\]
A. m = 3
B. \[3 - \sqrt 2 < m < 3 + \sqrt 2 \]
C. \[\left[ {\begin{array}{*{20}{c}}{m \ge 3 + \sqrt 2 }\\{m \le 3 - \sqrt 2 }\end{array}} \right.\]
D. Không tồn tại
Giải bởi Vietjack
Yêu cầu bài toán tương đương tìm giá trị của m để đồ thị hàm số
\[\left( P \right):y = 2{x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 4\] luôn nằm phía trên trên trục hoành.
Suy ra với giá trị x0 thì giá trị nhỏ nhất của hàm số đã cho lớn hơn hoặc bằng 0.
Parabol có hệ số a = 2 >0 nên có bề lõm hướng lên trên đạt GTNN tại đỉnh parabol \[x = \frac{{m + 1}}{2}\]
Điều này tương đương với \[y\left( {\frac{{m + 1}}{2}} \right) \ge 0\]
\[ \Leftrightarrow 2{\left( {\frac{{m + 1}}{2}} \right)^2} - 2\left( {m + 1} \right)\left( {\frac{{m + 1}}{2}} \right) + {m^2} - 2m + 4 \ge 0\]
\[ \Leftrightarrow \frac{1}{2}({m^2} - 6m + 7) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge 3 + \sqrt 2 }\\{m \le 3 - \sqrt 2 }\end{array}} \right.\]
Đáp án cần chọn là: C
Xác định Parabol (P):\[y = a{x^2} + bx - 5\] biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
Tìm các giá trị thực của tham số m để phương trình \[\left| {{x^2} - 3x + 2} \right| = m\;\] có bốn nghiệm thực phân biệt.
Cho đồ thị hàm số \[y = a{x^2} + bx + c\] như hình vẽ.
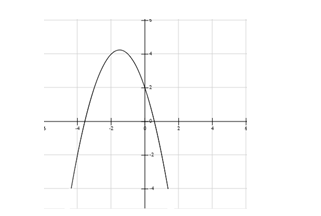
Khẳng định nào sau đây là đúng:
Xác định Parabol (P):\[y = a{x^2} + bx + 3\;\] biết rằng Parabol có đỉnh I(3;−2).
Tìm giá trị của m để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
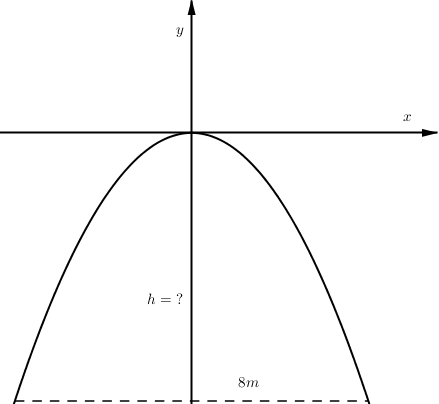
Một chiếc cổng parabol dạng \[y = - 12{x^2}\;\] có chiều rộng d = 8m. Hãy tính chiều cao h của cổng ?
Tìm các giá trị của tham số m để phương trình \[2{x^2} - 2x + 1 - m = 0\;\]có hai nghiệm phân biệt
Tìm các giá trị của tham số m để phương trình \[\frac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}\] có 3 nghiệm thực phân biệt.
Xác định Parabol (P):\[y = a{x^2} + bx + 2\;\] biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
Tìm các giá trị của tham số mm để phương trình \[{x^2} - 2(m + 1)x + 1 = 0\;\] có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).
Tìm giá trị nhỏ nhất của biểu thức \[P = 3\left( {\frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\frac{a}{b} + \frac{b}{a}} \right)\].
Tìm các giá trị của m để hàm số \[y = {x^2} + mx + 5\;\] luôn đồng biến trên \[\left( {1; + \infty } \right)\]
Tìm giá trị của m để hàm số \[y = - {x^2} + 2x + m - 5\] đạt giá trị lớn nhất bằng 6
Cho phương trình của (P):\[y = a{x^2} + bx + c\left( {a \ne 0} \right)\] biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tình tổng \[{a^2} + {b^2} + {c^2}\]
