Cho x;y là hai số thực dương thỏa mãn \[x \ne y\;\] và \[{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\]. Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\]
A.\[\min P = \frac{{13}}{2}.\]
B. \[\min P = \frac{9}{2}.\]
C. \[\min P = - 2.\]
D. \[\min P = 6.\]
Giải bởi Vietjack
Ta có
\[\begin{array}{*{20}{l}}{P = \frac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}}\\{ \Leftrightarrow Pxy - P{y^2} = {x^2} + 3{y^2}}\\{ \Leftrightarrow \left( {P + 3} \right){y^2} - Pxy + {x^2} = 0}\end{array}\]
Phương trình trên có nghiệm khi
\[\begin{array}{l}\Delta = {P^2}{x^2} - 4(P + 3){x^2} \ge 0\\ \Leftrightarrow {P^2} - 4P - 12 \ge 0\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{P \ge 6}\\{P \le - 2}\end{array}} \right. \Rightarrow MinP = 6\end{array}\]
Dấu bằng xáy ra khi\(\left\{ {\begin{array}{*{20}{c}}{y = \frac{{Px}}{{2(P + 3)}} = \frac{x}{3}}\\{\frac{{{x^2} + 3{y^2}}}{{xy - {y^2}}} = 6}\end{array}} \right. \Rightarrow x = 3y\)
Dễ thấy x=3y thỏa mãn điều kiện bài cho vì:
\[\begin{array}{l}{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\\ \Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^3}\\ \Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {2^{3y}} + \frac{1}{{{2^{3y}}}} + {3.2^y}.\frac{1}{{{2^y}}}.\left( {{2^y} + \frac{1}{{{2^y}}}} \right)\\ \Leftrightarrow 0 < 3\left( {{2^y} + \frac{1}{{{2^y}}}} \right)\end{array}\]
Bđt trên luôn đúng với mọi y>0.
Đáp án cần chọn là: D
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
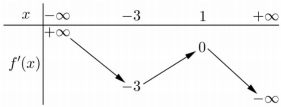
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
Nghiệm của bất phương trình \[{e^x} + {e^{ - x}} < \frac{5}{2}\] là
Tập hợp nghiệm của bất phương trình: \[{3^{3x - 2}} + \frac{1}{{{{27}^x}}} \le \frac{2}{3}\] là:
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
Cho hàm số \[f\left( x \right) = \frac{{{3^x}}}{{{7^{{x^2} - 4}}}}\]. Hỏi khẳng định nào sau đây là sai?
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\]
Có bao nhiêu giá trị thực của m để bất phương trình \[{4^x} - (m + 1){2^x} + m < 0\;\]vô nghiệm?
Tập nghiệm của bất phương trình \[{\left( {{x^2} + x + 1} \right)^x} < 1\] là:
Bất phương trình \[{\left( {2 - \sqrt 3 } \right)^x} > {\left( {2 + \sqrt 3 } \right)^{x + 2}}\]có tập nghiệm là:
