Có bao nhiêu giá trị thực của m để bất phương trình \[{4^x} - (m + 1){2^x} + m < 0\;\]vô nghiệm?
A.2
B.vô số
C.1
D.0
Giải bởi Vietjack
\[{4^x} - \left( {m + 1} \right){2^x} + m < 0\,\,\,\,\left( 1 \right)\]
Đặt\[{2^x} = t\,\,\left( {t > 0} \right).\]
Khi đó bất phương trình đã cho\[ \Leftrightarrow {t^2} - \left( {m + 1} \right)t + m < 0\,\,\,\left( * \right).\]
TH1:\[m = 1 \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 2t + 1 < 0 \Leftrightarrow {\left( {t - 1} \right)^2} < 0\]=> bất phương trình vô nghiệm.</>
⇒m=1 thỏa mãn.
TH2: \[m \ne 1\]
\[\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow {t^2} - mt - t + m < 0\\ \Leftrightarrow {t^2} - t - \left( {mt - m} \right) < 0\\ \Leftrightarrow t\left( {t - 1} \right) - m\left( {t - 1} \right) < 0\\ \Leftrightarrow \left( {t - 1} \right)\left( {t - m} \right) < 0\,\,\,\end{array}\]
+) Với m>1⇒ Tập nghiệm của bất phương trình là: \[S = \left( {1;\,\,m} \right) \subset \left( {0; + \infty } \right)\]
⇒ Bất phương trình (∗) luôn có nghiệm t>0
⇒(1) luôn có nghiệm xx ⇒m>1 không thỏa mãn.
+) Với m<1 ⇒ Tập nghiệm của bất phương trình là:\[S = \left( {m;\,\,1} \right)\]
⇒ Bất phương trình (∗) luôn có nghiệm 0<t<1
⇒(1) luôn có nghiệm x ⇒m<1 không thỏa mãn.
Vậy chỉ có m=1 thỏa mãn bài toán.
Đáp án cần chọn là: C
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
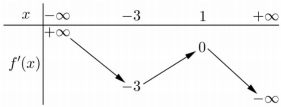
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
Nghiệm của bất phương trình \[{e^x} + {e^{ - x}} < \frac{5}{2}\] là
Tập hợp nghiệm của bất phương trình: \[{3^{3x - 2}} + \frac{1}{{{{27}^x}}} \le \frac{2}{3}\] là:
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
Cho hàm số \[f\left( x \right) = \frac{{{3^x}}}{{{7^{{x^2} - 4}}}}\]. Hỏi khẳng định nào sau đây là sai?
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\]
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
Bất phương trình \[{\left( {2 - \sqrt 3 } \right)^x} > {\left( {2 + \sqrt 3 } \right)^{x + 2}}\]có tập nghiệm là:
Tập nghiệm của bất phương trình \[{\left( {{x^2} + x + 1} \right)^x} < 1\] là:
Cho x;y là hai số thực dương thỏa mãn \[x \ne y\;\] và \[{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\]. Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\]
