Cho hàm số \[y = {x^4} - 2m{x^2} + {m^2} + m.\]. Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có một góc 120o là:
A.\[m = \frac{1}{{\sqrt[3]{3}}}\]
B. \[m = 0;\,m = \frac{1}{{\sqrt[3]{3}}}\]
C. \[m = \frac{1}{{\sqrt[3]{2}}}\]
D. \[m = 1\]
Giải bởi Vietjack
\[\begin{array}{l}y\prime = 4{x^3} - 4mx\\y\prime = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x({x^2} - m) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm \sqrt m }\end{array}} \right.\end{array}\]
Điều kiện để hàm số có 3 cực trị: m>0
\[\begin{array}{*{20}{l}}{x = 0 \Rightarrow A\left( {0;\,{m^2} + m} \right)}\\{x = - \sqrt m \Rightarrow y = {{\left( { - \sqrt m } \right)}^4} - 2m{{\left( { - \sqrt m } \right)}^2} + {m^2} + m}\\{ = {m^2} - 2{m^2} + {m^2} + m = m \Rightarrow B\left( { - \sqrt m ;\,m} \right)}\\{x = \sqrt m \Rightarrow C\left( {\sqrt m ;\,m} \right)}\end{array}\]
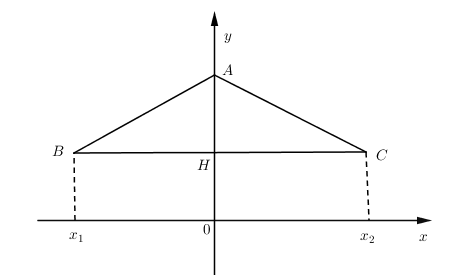
\[\begin{array}{l}\overrightarrow {AB} = ( - \sqrt m ; - {m^2}),\overrightarrow {AC} = (\sqrt m ; - {m^2})\\\widehat {BAC} = {120^0}\end{array}\]
\(\begin{array}{l} \Leftrightarrow \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = cos{120^0}\\ \Leftrightarrow \frac{{ - m + {m^4}}}{{\sqrt {m + {m^4}} .\sqrt {m + {m^4}} }} = - \frac{1}{2}\\ \Leftrightarrow 2({m^4} - m) = - (m + {m^4})\\ \Leftrightarrow 3{m^4} - m = 0\\ \Leftrightarrow m(3{m^3} - 1) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0(loai)}\\{m = \frac{1}{{\sqrt[3]{3}}}}\end{array}} \right.\end{array}\)
Đáp án cần chọn là: A
Tìm m để (Cm) : \[y = {x^4} - 2m{x^2} + 2\;\] có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân.
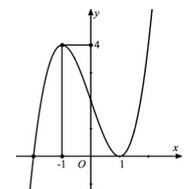
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm \[g\prime (x) = f(x) + m\]. Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.
Tìm tất cả các giá trị của m để hàm số \[y = \frac{{m{x^3}}}{3} - m{x^2} + x - 1\] có cực đại và cực tiểu.
Cho hàm số \[y = 2{x^4} - \left( {m + 1} \right){x^2} - 2.\]. Tất cả các giá trị của m để hàm số có 1 điểm cực trị là:
Cho hàm số \[y = {x^4} - 2m{x^2} + 3m + 2.\]. Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác đều là:
Tìm tất cả các giá trị của tham số m để hàm số \[y = {x^3} - 2m{x^2} + {m^2}x + 2\;\] đạt cực tiểu tại x=1.
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \[y = \mid 3{x^4} - 4{x^3} - 12{x^2} + m\mid \;\] có 5 điểm cực trị?
Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số \[y = {x^3} + 3m{x^2} - 3x\]
Gọi \[{m_0}\] là giá trị của mm thỏa mãn đồ thị hàm số \[y = \frac{{{x^2} + mx - 5}}{{{x^2} + 1}}\] có hai điểm cực trị A,B sao cho đường thẳng AB đi qua điểm I(1;−3). Khẳng định nào sau đây là đúng?
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \[y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\] có hai điểm cực trị nằm về hai phía của trục hoành.
Hàm số \[f\left( x \right) = \left| {\frac{x}{{{x^2} + 1}} - m} \right|\] (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
Tìm tất cả các giá trị của m để đồ thị hàm số \[y = - {x^4} + 2m{x^2}\;\] có 3 điểm cực trị ?
Cho hàm số \[y = {x^4} + 2\left( {1 - {m^2}} \right){x^2} + m + 1.\]. Tất cả các giá trị của mm để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có diện tích bằng \(4\sqrt 2 \)là
Cho hàm số \[y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.\]. Tìm mm để đồ thị hàm số có hai điểm cực trị là A,B sao cho đường thẳng AB vuông góc với \[d:x - y - 9 = 0\]
Cho hàm số \[y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6\] với mm là tham số thực. Tìm tất cả các giá trị của m để hàm số có hai điểm cực trị \[{x_1},{x_2}\] thỏa mãn \[{x_1} < - 1 < {x_2}\]
