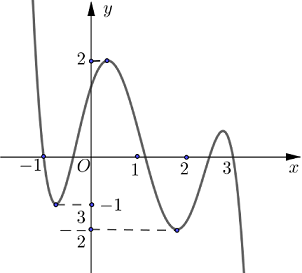
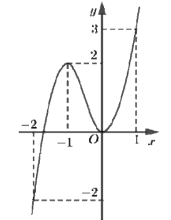
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f(1 - 2cosx)\] trên \[\left[ {0;\frac{{3\pi }}{2}} \right].\]Giá trị của M+m bằng
A.\(\frac{1}{2}\)
B. \(\frac{3}{2}\)
C. 2
D. 1
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt\[t = 1 - 2\cos x\]Với \[x \in \left[ {0;\,\,\frac{{3\pi }}{2}} \right]\]thì\[\cos x \in \left[ { - 1;1} \right] \Rightarrow 1 - 2\cos x \in \left[ { - 1;3} \right] \Rightarrow t \in \left[ { - 1;3} \right].\]
Khi đó ta có \[y = f\left( t \right)\]với \[t \in \left[ { - 1;3} \right]\]
Quan sát đồ thị hàm số\[y = f\left( t \right)\]trên đoạn\[\left[ { - 1;3} \right]\]ta thấy GTLN của hàm số là 2, GTNN của hàm số là \[ - \frac{3}{2}\]
\[ \Rightarrow M = 2,\,\,m = - \frac{3}{2} \Rightarrow M + m = \frac{1}{2}\]
Đáp án cần chọn là: A
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=sinx trên đoạn \[[ - \frac{\pi }{2}; - \frac{\pi }{3}]\] lần lượt là
Giá trị nhỏ nhất của hàm số \[y = 2x + \cos x\] trên đoạn \[\left[ {0;1} \right]\;\]là :
Cho hàm số f(x) xác định và liên tục trên R, có \[\mathop {\lim }\limits_{x \to + \infty } = + \infty ;\mathop {\lim }\limits_{x \to - \infty } = - \infty \] , khi đó:
Cho hàm số f(x) xác định trên \[\left[ {0;2} \right]\;\]và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
Cho biết GTLN của hàm số f(x) trên \[\left[ {1;3} \right]\;\]là M=−2. Chọn khẳng định đúng:
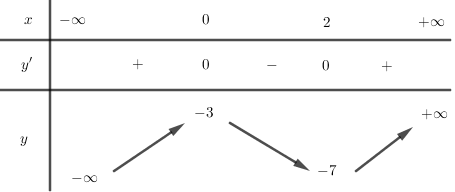
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
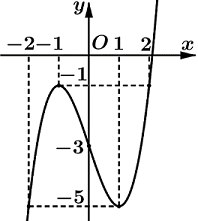
Cho hàm số y=f(x)) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn \[\left[ { - 2;2} \right]\]
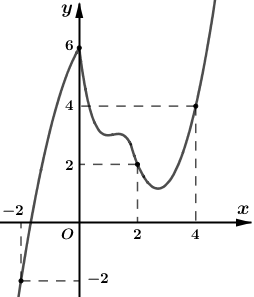
Cho hàm số \[y = {x^3} - 3m{x^2} + 6\], giá trị nhỏ nhất của hàm số trên \[\left[ {0;3} \right]\;\]bằng 2 khi:
Cho hàm số \[y = x + \frac{1}{x}.\] Giá trị nhỏ nhất của hàm số trên khoảng \[\left( {0; + \infty } \right)\;\]là:
Cho \[f\left( x \right) = \frac{1}{{{x^2} - 4x + 5}} - \frac{{{x^2}}}{4} + x\] Gọi \[M = \mathop {Max}\limits_{x \in \left[ {0;3} \right]} f(x);\;m = \mathop {Min}\limits_{x \in \left[ {0;3} \right]} f\left( x \right)\] Khi đó M−m bằng:
Đề thi THPT QG - 2021 - mã 101
Trên đoạn \[\left[ {0;3} \right],\]hàm số \[y = - {x^3} + 3x\;\] đạt giá trị lớn nhất tại điểm
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) có đồ thị \[y = f\prime (x)\;\] như hình vẽ. Đặt \[g(x) = 2f(x) - {x^2}\]. Khi đó giá trị lớn nhất của hàm số g(x) trên đoạn \[\left[ { - 2;4} \right]\;\]là:
Giá trị lớn nhất của hàm số \[f\left( {\rm{x}} \right) = \frac{{6 - 8{\rm{x}}}}{{{x^2} + 1}}\] trên tập xác định của nó là:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi a,A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của f(x+1) trên đoạn \[\left[ { - 1;0} \right].\;\]Giá trị a+A bằng:
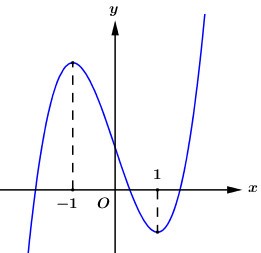
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình bên:
Giá trị nguyên lớn nhất của tham số m để hàm số \[y = f(|x| - m)\;\] đồng biến trên khoảng \[\left( {10; + \infty } \right)\;\]là: