Có bao nhiêu giá trị xϵ[0; 5π] để hàm số y = tanx nhận giá trị bằng 0?
A. 9
B. 10
C. 7
 Giải bởi Vietjack
Giải bởi Vietjack
Ta vẽ đồ thị hàm số y = tanx trên đoạn [0;5π].
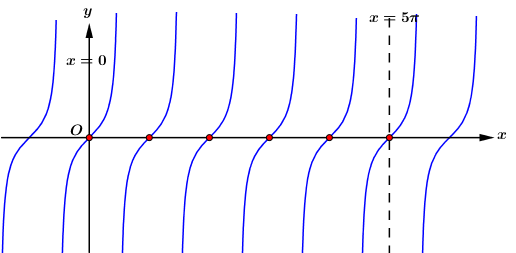
Dựa vào đồ thị hàm số ta thấy trên đoạn [0;5π], đồ thị hàm số cắt trục hoành tại 6 điểm phân biệt (điểm màu đỏ), do đó có 6 giá trị xϵ[0;5π] để hàm số y = tanx nhận giá trị bằng 0.
Đáp án cần chọn là: D
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?
y = 2sin2 x + cos2 2x:
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 3sinx + 4cosx − 1
Cho các mệnh đề sau :
(I): Hàm số y = sinx có chu kì là .
(II): Hàm số y = tanx có tập giá trị là R∖
(III): Đồ thị hàm số y = cosx đối xứng qua trục tung.
(IV): Hàm số y = cotx nghịch biến trên (−π; 0)
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên ?
Xét sự biến thiên của hàm số y = sinx − cosx. Trong các kết luận sau, kết luận nào đúng?