Khẳng định nào sau đây là đúng?
A. y = |tanx| đồng biến trong
B. y = |tanx| là hàm số chẵn trên D = R\
C. y = |tanx| có đồ thị đối xứng qua gốc tọa độ.
Giải bởi Vietjack
Ta có đồ thị hàm số y = |tanx| như sau:
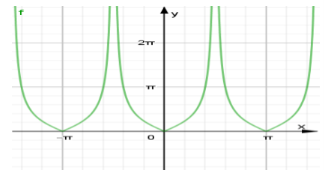
TXĐ: D = R\
Dựa vào đồ thị hàm số ta thấy:
- Hàm số y = |tanx| nghịch biến trên và đồng biến trên ,do đó đáp án A và D sai.
- Đặt f(x) = |tanx|, ∀x∈D ⇒ −x∈D
f(−x) = |tan(−x)| = |−tanx| = |tanx| = f(x), do đó hàm số đã cho là hàm chẵn trên tập xác định. Do đó đáp án B đúng.
- Do là hàm chẵn nên đồ thị hàm số đối xứng qua trục Oy chứ không đối xứng qua tâm O, do đó đáp án C sai.
Đáp án cần chọn là: B
y = 2sin2 x + cos2 2x:
Cho các mệnh đề sau :
(I): Hàm số y = sinx có chu kì là .
(II): Hàm số y = tanx có tập giá trị là R∖
(III): Đồ thị hàm số y = cosx đối xứng qua trục tung.
(IV): Hàm số y = cotx nghịch biến trên (−π; 0)
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên ?
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 3sinx + 4cosx − 1
Xét sự biến thiên của hàm số y = sinx − cosx. Trong các kết luận sau, kết luận nào đúng?
